Presanis, De Angelis, Goubar, Gill and Ades have a new
paper in Biostatistics. The paper attempts to use several disparate sources of data on prevalence and incidence to estimate transition rates and prevalences in a multi-state model of transmission of HIV among men who have sex with men (ironically abbreviated as MSM) via Bayesian evidence synthesis. The multi-state model has 4 transient states relating to "Eligible (non MSM)", "Susceptible (MSM)", "Undiagnosed" and "Diagnosed". Subjects enter aged 15 (or later due to migration) and may exit due to death or reaching age 45.
It should be noted that the multi-state model is deterministic and not stochastic, i.e. the proportions in each state at a given time conditional on the parameters and starting conditions are the solution of an ordinary differential equation. While this is unproblematic in terms of getting estimates of the expected proportions in each state at a given time, there must be some level of under representation of the uncertainty. In particular the likelihood assumes that the number of deaths from HIV from the SOPHID dataset at time
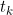
is
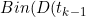,\gamma_D(t_{k-1})))
where
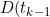)
is the number in the diagnosed state at time
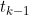
and
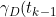))
is the probability of death in one year from HIV for the year
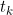
. In reality D(t) should be stochastic rather than deterministic and as such we would expect the number of deaths to have a higher variance than assumed by the binomial model.
In principle the covariance matrix of the numbers in each state for each year could be derived, i.e. given the Markov model, we have N independent individuals each of whom's state occupancy at time
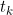
is multinomial given the occupancy at time
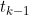
. A more realistic model would then assume that conditional on the parameters, the state occupation counts have a multivariate normal distribution (e.g. analogous to the approaches taken in the estimation of
aggregate Markov data) and, for instance, the number of deaths from HIV is binomial with a denominator that is itself normally distributed. Quite possibly this extra source of uncertainty is negligible compared to the vast existing uncertainties but it nevertheless ought to be explored.
No comments:
Post a Comment