Non-homogeneous Markov process models with informative observations with an application to Alzheimer's disease

Baojiang Chen and Xiao-Hua Zhou have a new paper in Biometrical Journal. The methodological development of the paper is to extend the methods of Chen, Yi and Cook (Stat Med, 2010) to the case of a non-homogeneous Markov model using the time transformation model of Hubbard et al (Biometrics, 2008) rather than the piecewise constant intensities used in Chen, Yi and Cook. The authors claim that the time transformation model is more appealing than piecewise constant intensities because it requires fewer parameters. However, this parsimony is at the cost of flexibility, as the time transformation model assumes the same temporal trend for all intensities.

The assumption of non-informative examination times is an ever present spectre for multi-state models from panel data. Chen et al's method provides some methods when a complete set of planned examination times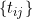 is known and it is simply the case that some examination times are missed, meaning the problem can be dealt within the Rubin framework of MAR/MNAR. A more general situation would be where the multi-state process and the process that generates the examination times are dependent. Here the only option seems to be to jointly model the two processes explicitly. A starting model might be one where the intensities of the counting process generating the examination times and the multi-state model are linked through a joint frailty, e.g. something analogous to models for joint modelling of longitudinal and (informative) drop-out (survival) processes.