Nicola Bartolomeo, Paolo Trerotoli and Gabriella Serio have a new
paper in BMC Medical Research Methodology. This applies a three state hidden Markov model to data on the progression of liver cirrhosis to Hepatocellular carcinoma. A time homogeneous continuous time progressive model is fitted with death as the absorbing state. Covariate effects are included via a proportional intensities model.
Schoenfeld residuals, which are appropriate for right censored data, are applied here as a test of proportionality. It isn't made clear precisely how this is done here. If time of death is known exactly then a Schoenfeld type residual could be defined for the times of death replacing the standard formulation
}}{\sum_{u \in R_j} \exp{(\hat{\beta} x_{uj})}} "x_{ij} - \frac{\sum_{u \in R_j} x_{uj} \exp{(\hat{\beta} x_{uj})}}{\sum_{u \in R_j} \exp{(\hat{\beta} x_{uj})}}")
with
/dt}{\sum_{u \in R_j} dP_{3}(t_j,x_{uj};\hat{\beta})/dt} "x_{ij} - \frac{\sum_{u \in R_j} x_{uj} dP_{3}(t_j,x_{uj};\hat{\beta})/dt}{\sum_{u \in R_j} dP_{3}(t_j,x_{uj};\hat{\beta})/dt}")
where
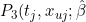 = P(X(t_j) = 3 | X(0)=1, x_{uj}, \hat{\beta}). "\inline P_{3}(t_j,x_{uj};\hat{\beta}) = P(X(t_j) = 3 | X(0)=1, x_{uj}, \hat{\beta}).")
If the times of death are interval censored then this approach is inappropriate.
On a more trivial level the matrix of misclassification probabilities is missing a 1 in the third row corresponding to the absorbing state.
No comments:
Post a Comment