Juha Mehtala ,Kari Auranen and Sangita Kulathina have a new paper in Statistical Methods in Medical Research. This considers optimal design of panel studies for binary stochastic processes which are assumed to be time-homogeneous Markov. Optimality is assessed based on the trace of the expected Fisher information. The authors also consider a two-phase design where the time spacing is improved upon after the first stage.
This paper, and also the paper by Hwang and Brookmeyer, restrict attention to equally spaced designs. Potentially, there may be efficiency gains from having unequally spaced observations particularly if equilibrium is not assumed at time 0. Moreover, an adaptive "doctor's care" type design where the gap to the next clinic visit depends on the current state is also likely to give some efficiency gains. There has been relatively little work on design for multi-state models. Clearly the efficiency gains achieved in practice depend on the accuracy of the initial assumptions about the true parameter values, although if a two-phase approach is possible it can militate against this. In complicated studies a simple relationship between expected parameter values and optimal design may not exist but may nevertheless be calculable by bespoke numerical optimization. Perhaps the main problem is that studies are rarely designed with an eventual multi-state model analysis in mind.
Friday, 23 December 2011
Tuesday, 13 December 2011
A dynamic model for the risk of bladder cancer progression
Núria Porta, M. Luz Calle, Núria Malats and Guadalupe Gómez have a new paper in Statistics in Medicine. This develops a model for progression of bladder cancer with particular emphasis on predicting future risk given events up to a certain point in time.
In many ways the paper is taking a similar approach to Cortese and Andersen in explicitly modelling a time dependent covariate (here recurrence) in order to obtain predictions.
They fit a semi-parametric Cox Markov multi-state model to the data and define a prediction process
 = P(t < T_2 \leq u, C_2 = P | H(t)) "\pi(u,t) = P(t < T_2 \leq u, C_2 = P | H(t))")
where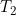
is the time of the second event, 
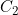is the type of the second event where P denotes progression and  "\inline H(t)")
represents the history of the process up to time t. Analogously to outcome measures like the cumulative incidence functions, this predictive process is a function of the transition intensities. They also consider time dependent ROC curves to assess the improvement in classification accuracy that can be achieved by taking into account past history in addition to baseline characteristics.
In many ways the paper is taking a similar approach to Cortese and Andersen in explicitly modelling a time dependent covariate (here recurrence) in order to obtain predictions.
They fit a semi-parametric Cox Markov multi-state model to the data and define a prediction process
where
Wednesday, 7 December 2011
Estimating net transition probabilities from cross-sectional data with application to risk factors in chronic disease modeling
van de Kassteele, Hoogenveen, Engelfriet, van Baal and Boshuizen have a new paper in Statistics in Medicine. This considers the estimation of the transition probabilities in a non-homogeneous discrete-time Markov model, when the only available information is cross-sectional data, i.e. for each time (or age) we have only a sample of individuals and their state occupancy from which the prevalence at that time can be estimated. Note this type of observation is more extreme than aggregate data, considered for instance by Crowder and Stephens, where we only have prevalences at a series of times but the state occupation counts correspond to the same set of subjects.
The authors take a novel, if slightly quirky approach, to estimation. They firstly use P-splines to smooth the observed prevalences. Having obtained these they then need to translate them into transition probabilities. This is not straightforward since there are more parameters to estimate than degrees of freedom. To get around this problem the authors restrict their estimate to be the values that minimize a transportation problem. Essentially this assigns a "cost" to transitions, penalizing those to further apart states and giving zero cost to remaining in the same state. So gives a solution that aims to maximize the diagonals of the transition probability matrices whilst constraining the prevalences to take their P-spline smoothed values.
What is absent from the paper is formal justification for the approach. Presumably a similar outcome could be achieved by applying a penalized likelihood approach, possibly formulating the problem in continuous time and setting the penalty to be the magnitude of the transition intensities (and possibly their derivatives). However, this would require some calibration to choose the penalty weights and it is not clear how this would be done (the usual approach of cross-validation would not work here).
The authors take a novel, if slightly quirky approach, to estimation. They firstly use P-splines to smooth the observed prevalences. Having obtained these they then need to translate them into transition probabilities. This is not straightforward since there are more parameters to estimate than degrees of freedom. To get around this problem the authors restrict their estimate to be the values that minimize a transportation problem. Essentially this assigns a "cost" to transitions, penalizing those to further apart states and giving zero cost to remaining in the same state. So gives a solution that aims to maximize the diagonals of the transition probability matrices whilst constraining the prevalences to take their P-spline smoothed values.
What is absent from the paper is formal justification for the approach. Presumably a similar outcome could be achieved by applying a penalized likelihood approach, possibly formulating the problem in continuous time and setting the penalty to be the magnitude of the transition intensities (and possibly their derivatives). However, this would require some calibration to choose the penalty weights and it is not clear how this would be done (the usual approach of cross-validation would not work here).
Intermittent observation of time-dependent explanatory variables: a multistate modelling approach
Brian Tom and Vern Farewell have a new paper in Statistics in Medicine. This considers the problem of estimating the effect of a time dependent covariate on a multi-state process when both the disease process of interest and the time dependent covariate are only intermittently observed. The most common existing approach to dealing with this problem is to assume that the time dependent covariate is constant between observations, taking the last observed value. The authors instead jointly model the two processes as an expanded multi-state model, if the disease process had n states and the covariate process m states the resulting process will have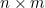 
states. An additional assumption, that movements in the covariate process are not directly affected by the state of the disease process, is also made.
A simulation study is performed which shows that the approach of assuming the time dependent covariate is constant leads to biased estimates, particularly when there is a bias in the trend of the covariate process (e.g. much more likely to decrease than increase in value).
The overall approach taken by the authors is to model their way out of difficulty. They assume that both the disease process of interest and the covariate process are jointly time homogeneous Markov and the validity of the results will depend on these assumptions being correct. As noted by the authors, if the covariate can take more than a small number of values the approach becomes unattractive because of the large number of nuisance parameters required. A point not really emphasized, but related to the analogous approach taken by Cortese and Andersen for continuously observed competing risks data (bizarrely not referenced in this paper despite massive relevance!), is that having modelled the time dependent covariate, the model can then be used to make overall predictions.
One could argue that the convention of following forward the covariate value observed from the previous period is a way of allowing a prediction to be made about the trajectory in the next period. A fairer comparison in some cases might therefore be to look at the bias in estimating the transition probabilities to time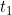
given a covariate variate value of 
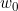at time 
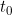. While we would expect these estimates still to be biased, the amount of bias is likely to be less than found by looking at the regression coefficients directly.
An open problem seems to be the development of methods that do not require strong assumptions, or else are robust to misspecification, to deal with intermittently observed time dependent covariates.
A simulation study is performed which shows that the approach of assuming the time dependent covariate is constant leads to biased estimates, particularly when there is a bias in the trend of the covariate process (e.g. much more likely to decrease than increase in value).
The overall approach taken by the authors is to model their way out of difficulty. They assume that both the disease process of interest and the covariate process are jointly time homogeneous Markov and the validity of the results will depend on these assumptions being correct. As noted by the authors, if the covariate can take more than a small number of values the approach becomes unattractive because of the large number of nuisance parameters required. A point not really emphasized, but related to the analogous approach taken by Cortese and Andersen for continuously observed competing risks data (bizarrely not referenced in this paper despite massive relevance!), is that having modelled the time dependent covariate, the model can then be used to make overall predictions.
One could argue that the convention of following forward the covariate value observed from the previous period is a way of allowing a prediction to be made about the trajectory in the next period. A fairer comparison in some cases might therefore be to look at the bias in estimating the transition probabilities to time
An open problem seems to be the development of methods that do not require strong assumptions, or else are robust to misspecification, to deal with intermittently observed time dependent covariates.
Monday, 28 November 2011
Frailties in multi-state models: Are they identifiable? Do we need them?
Hein Putter and Hans van Houwelingen have a new paper in Statistical Methods in Medical Research. This reviews the use of frailties within multi-state models, concentrating on the case of models observed up to right-censoring and primarily looking at models where the semi-Markov (Markov renewal) assumption is made. The paper clarifies some potential confusion over when frailty models are identifiable. For instance, for simple survival data with no covariates, if a non-parametric form is taken for the hazard then no frailty distribution is identifiable. A similar situation is true for competing risks data. Things begin to improve once we can observe multiple events for each patient (e.g. in illness-death models), although clearly if the baseline hazard is non-parametric, some parametric assumptions will be required for the frailty distribution. When covariates are present in the model, the frailty term has a dual role of modelling dependence between transition times but also soaking up lack of fit in the covariate (e.g. proportional hazards) model.
The authors consider two main approaches to fitting a frailty; assuming a shared Gamma frailty which acts as a multiplier on all the intensities of the multi-state model and a two-point mixture frailty, where there are two mixture components with a corresponding set of multiplier terms for the intensities for each component. Both approaches admit a closed form expression for the marginal transition intensities and so are reasonably straightforward to fit, but the mixture approach has the advantage of permitting a greater range of dependencies, e.g. it can allow negative as well as positive correlations between sojourn times.
In the data example the authors consider the predictive power (via K-fold cross-validation) of a series of models on a forward (progressive) multi-state model. In particular they compare models which allow sojourn times in later states to depend on the time to first event, with frailty models and find the frailty model performs a little better. Essentially, these two models do the same thing and as the authors note, a more flexible model for the effect of time of first event on the second sojourn time may well give a better fit than the frailty model.
Use of frailties in models with truly recurrent events seems relatively uncontroversial. However for models where few intermediate events are possible their use, rather than some non-homogeneous model allowing dependence both on time since entry to the state and time since initiation, the choice is largely related to either what is more interpretable in terms of the application at hand or possibly what is more computationally convenient.
The authors consider two main approaches to fitting a frailty; assuming a shared Gamma frailty which acts as a multiplier on all the intensities of the multi-state model and a two-point mixture frailty, where there are two mixture components with a corresponding set of multiplier terms for the intensities for each component. Both approaches admit a closed form expression for the marginal transition intensities and so are reasonably straightforward to fit, but the mixture approach has the advantage of permitting a greater range of dependencies, e.g. it can allow negative as well as positive correlations between sojourn times.
In the data example the authors consider the predictive power (via K-fold cross-validation) of a series of models on a forward (progressive) multi-state model. In particular they compare models which allow sojourn times in later states to depend on the time to first event, with frailty models and find the frailty model performs a little better. Essentially, these two models do the same thing and as the authors note, a more flexible model for the effect of time of first event on the second sojourn time may well give a better fit than the frailty model.
Use of frailties in models with truly recurrent events seems relatively uncontroversial. However for models where few intermediate events are possible their use, rather than some non-homogeneous model allowing dependence both on time since entry to the state and time since initiation, the choice is largely related to either what is more interpretable in terms of the application at hand or possibly what is more computationally convenient.
Sunday, 20 November 2011
Isotonic estimation of survival under a misattribution of cause of death
Jinkyung Ha and Alexander Tsodikov have a new paper in Lifetime Data Analysis. This considers the problem of estimation of the cause specific hazard of death from a particular cause in the presence of competing risks and misattribution of cause of death. They assume they have right-censored data for which there is an associated cause of death, but that there is some known probability r(t) of misattributing the cause of death from a general cause to a specific cause (in this case pancreatic cancer) at time t.
The authors consider four estimators for the true underlying cause-specific hazards. Firstly they consider a naive estimator which obtains Nelson-Aalen estimates of the observed CSHs and transforms them to true hazards by solving the implied equations
 &=& r(t)d\Lambda_{2}(t) + d\Lambda_{1}(t)\\ d\hat{\Lambda}^{Obs}_{2}(t) &=& (1-r(t))d\Lambda_{2}(t)\\ \end{matrix} "\begin{matrix} d\hat{\Lambda}^{Obs}_{1}(t) &=& r(t)d\Lambda_{2}(t) + d\Lambda_{1}(t)\\ d\hat{\Lambda}^{Obs}_{2}(t) &=& (1-r(t))d\Lambda_{2}(t)\\ \end{matrix}")
This estimator is unbiased but has the drawback that there are negative increments to the cause-specific hazards.
The second approach is to apply a (constrained) NPMLE estimate for instance via an EM algorithm. The authors show that, unless the process is in discrete time (such that the number of failures at a specific time point increases as the sample size increases), this estimator is asymptotically biased.
The third and fourth approaches take the naive estimates and apply post-hoc algorithms to ensure monotonicity of the cumulative hazards, by using the maximum observed naive cumulative hazard up to time t (sup-estimator) or by applying the pool-adjacent-violators algorithm to the naive cumulative hazard. These estimators have the advantage of being both consistent and guaranteed to be monotonic.
The authors consider four estimators for the true underlying cause-specific hazards. Firstly they consider a naive estimator which obtains Nelson-Aalen estimates of the observed CSHs and transforms them to true hazards by solving the implied equations
This estimator is unbiased but has the drawback that there are negative increments to the cause-specific hazards.
The second approach is to apply a (constrained) NPMLE estimate for instance via an EM algorithm. The authors show that, unless the process is in discrete time (such that the number of failures at a specific time point increases as the sample size increases), this estimator is asymptotically biased.
The third and fourth approaches take the naive estimates and apply post-hoc algorithms to ensure monotonicity of the cumulative hazards, by using the maximum observed naive cumulative hazard up to time t (sup-estimator) or by applying the pool-adjacent-violators algorithm to the naive cumulative hazard. These estimators have the advantage of being both consistent and guaranteed to be monotonic.
Monday, 14 November 2011
Likelihood based inference for current status data on a grid
Runlong Tang, Moulinath Banerjee and Michael Kosorok have a new paper in the Annals of Statistics. This considers the problem of non-parametric inference for current status data when the set of observation times is a grid of points such that multiple individuals can have the same observation time. This is distinct from the scenario usually considered in the literature where the observation times are generated from a continuous distribution, such that the unique number of observation times, K, is equal to the number of subjects, n. In this case, non-standard (Chernoff) asymptotics with a convergence rate of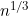 
applies. A straightforward alternative situation is where the total number of possible observation times has a fixed K. Here, standard Normal 
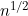asymptotics apply as n tends to infinity (though n may need to be much larger than K for approximations based on this to have much practical validity).
The authors consider a middle situation where K is allowed to increase with n at rate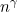
. They show that provided 
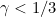, standard 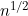asymptotics apply, whereas when 
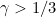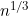, the asymptotics of the continuous observation scheme prevail. Essentially for 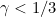, the NPMLE at each grid time point tends to its naive estimator (i.e. the proportion of failures at that time among those subjects observed there) and the isotonization has no influence. Whereas for 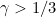there will continue to be observation times sufficiently "close" but distinct such that the isotonization will have an effect. A special boundary case applies when 
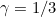, with an asymptotic distribution depending on c where c determines the spacing between grid points via 
.
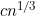Having established these facts, the authors then develop an adaptive inference method for estimating F at a fixed point. They suggest a simple estimator for c, based on the assumption that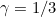
. The estimator has the property that c will tend to 0 if 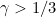and tend to infinity if 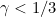. Concurrently, it can be shown that the limiting distribution for the case 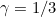tends to the standard normal distribution as c tends to infinity and tends to the Chernoff distribution when c goes to 0. As a consequence, constructing confidence intervals by assuming the 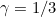asymptotics but with c estimated, will give valid asymptotic confidence intervals regardless of the true value of 
.
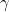There are some practical difficulties with the approach as the error distribution of the NPMLE of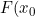 "\inline F(x_{0})")
depends both on 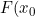and the sampling distribution density  "\inline g(x_{0})")
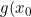as well as c. Moreover, whereas for 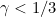, there is scaling invariance such that one can express the errors in terms of a function of an indexable distribution (i.e. the Chernoff distribution). The boundary distribution for 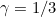does not admit such scaling so would require bespoke simulations to establish for each case.
The authors consider a middle situation where K is allowed to increase with n at rate
Having established these facts, the authors then develop an adaptive inference method for estimating F at a fixed point. They suggest a simple estimator for c, based on the assumption that
There are some practical difficulties with the approach as the error distribution of the NPMLE of
Bayesian inference for an illness-death model for stroke with cognition as a latent time-dependent risk factor
Van den Hout, Fox and Klein Entink have a new paper in Statistical Methods in Medical Research. This looks at joint modelling of cognition data measured through the Mini-Mental State Examination (MMSE) and stroke/survival data modelled as a three-state illness-death model. The MMSE produces item response type data and the longitudinal aspects are modelled through a latent growth model (with random slope and intercept). The three-state multi-state model is Markov conditional on the latent cognitive function. Time non-homogeneity is accounted for in a somewhat crude manner by pretending that age and cognitive function vary with time in a step-wise fashion.
The IRT model for MMSE allows the full information from the item response data to be used (e.g. rather than summing responses to individual questions to get a score). Similarly, compared to treating MMSE as an external time dependent covariate, the current model allows prediction of the joint trajectory of stroke and cognition. However, the usefulness of these predictions are constrained by how realistic the model actually is. The authors make the bold claim that the fact that a stroke will cause a decrease in cognition (which is not explicitly accounted for in their model) does not invalidate their model. It is difficult to see how this can be the case. The model constrains the decline in cognitive function to be linear (with patient specific random slope and intercept). If it actually falls through a one-off jump, then the model will still try to fit a straight line to a patient's cognition scores. Thus the cognition before the drop will tend to be down-weighted. It is therefore quite feasible that the result that lower cognition causes strokes is mostly spurious. One possible way of accommodating the likely effect of a stroke on cognition would be to allow stroke status to be a covariate in the linear growth model e.g. for multi-state process "\inline X(t)")
and latent trait  "\inline \theta(t)")
, we would take
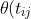 = \beta_0 + \beta_1 t_{ij} + \beta_2 I(X(t_{ij})=2) "\theta(t_{ij}) = \beta_0 + \beta_1 t_{ij} + \beta_2 I(X(t_{ij})=2)")
where the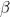
may be correlated random effects.
The IRT model for MMSE allows the full information from the item response data to be used (e.g. rather than summing responses to individual questions to get a score). Similarly, compared to treating MMSE as an external time dependent covariate, the current model allows prediction of the joint trajectory of stroke and cognition. However, the usefulness of these predictions are constrained by how realistic the model actually is. The authors make the bold claim that the fact that a stroke will cause a decrease in cognition (which is not explicitly accounted for in their model) does not invalidate their model. It is difficult to see how this can be the case. The model constrains the decline in cognitive function to be linear (with patient specific random slope and intercept). If it actually falls through a one-off jump, then the model will still try to fit a straight line to a patient's cognition scores. Thus the cognition before the drop will tend to be down-weighted. It is therefore quite feasible that the result that lower cognition causes strokes is mostly spurious. One possible way of accommodating the likely effect of a stroke on cognition would be to allow stroke status to be a covariate in the linear growth model e.g. for multi-state process
where the
Thursday, 3 November 2011
Relative survival multistate Markov model
Ella Huszti, Michal Abrahamowicz, Ahmadou Alioum, Christine Binquet and Catherine Quantin have a new paper in Statistics in Medicine. This develops a illness-death Markov model with piecewise constant intensities in order to fit a relative survival model. Such models seek to compare the mortality rates from disease states with those in the general population, so that the hazard from state r to absorbing state D are given by
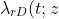 = \lambda_{\mbox{pop}}(t ; z) + \lambda^{*}_{rD}(t)\exp(\beta_{rD} z) "\lambda_{rD}(t ; z) = \lambda_{\mbox{pop}}(t ; z) + \lambda^{*}_{rD}(t)\exp(\beta_{rD} z)")
The population hazard is generally assumed known and taken from external sources like life tables. Transition intensities between transient states in the Markov model are not subject to any such restrictions. One can think this as being a model where there is an unobservable cause of death state "death from natural causes" which has the same transition intensity regardless of the current transient state.
The paper has quite a lot of simulation results, most of which seem unnecessary. They simulate data from the relative survival model and show, unsurprisingly, that a misspecified model that assumes proportionality with respect to the whole hazard (rather than the excess hazard) is biased. They also compare the results with Cox regression models (on each transition intensity) and Lunn-McNeil competing risks model (i.e. assuming a Cox model assuming common baseline for the competing risks).
The data are a mixture of clinic visits that yield interval censored times of events such as recurrence, but times of death are known exactly. Presumably for the Cox models a further approximation of interval-censored to right-censored data is made.
The population hazard is generally assumed known and taken from external sources like life tables. Transition intensities between transient states in the Markov model are not subject to any such restrictions. One can think this as being a model where there is an unobservable cause of death state "death from natural causes" which has the same transition intensity regardless of the current transient state.
The paper has quite a lot of simulation results, most of which seem unnecessary. They simulate data from the relative survival model and show, unsurprisingly, that a misspecified model that assumes proportionality with respect to the whole hazard (rather than the excess hazard) is biased. They also compare the results with Cox regression models (on each transition intensity) and Lunn-McNeil competing risks model (i.e. assuming a Cox model assuming common baseline for the competing risks).
The data are a mixture of clinic visits that yield interval censored times of events such as recurrence, but times of death are known exactly. Presumably for the Cox models a further approximation of interval-censored to right-censored data is made.
Thursday, 20 October 2011
Impact of delayed diagnosis time in estimating progression rates to hepatitis C virus-related cirrhosis and death
Bo Fu, Wenbin Wang and Xin Shi have a new paper in Statistical Methods in Medical Research. The paper is interested in the estimation of rates of progression from hepatitis C infection to cirrhosis and from cirrhosis to death. The primary complication in the model is that the time of cirrhosis development is interval censored, since it is only diagnosed at clinic examination times.
The model consists of a simple unidirectional 3-state model. A parametric Weibull approach is taken, where the time to cirrhosis from infection has a standard Weibull distribution and the time from cirrhosis to death has a Weibull distribution where the scale parameter is a function of the time between infection and cirrhosis.
Unsurprisingly, they show that a full likelihood approach which takes into account the interval censoring is much less biased than an approach that ignores the problem of interval censoring.
A criticism of the model, which the authors acknowledge, is that the possibility of death before cirrhosis is not accommodated. Potentially, even under their current model there might also be cases where death occurs after cirrhosis but before diagnosis of cirrhosis - a scenario which isn't accommodated in the three cases listed in their likelihood development. The rate of increase of the hazard of cirrhosis from infection is observed to increase after 30 years since infection. It is not clear whether this is a real effect, whether it is due to a small number of people at risk or whether it is an artifact of not accommodating the possibility of death without cirrhosis. Given the long follow-up time in the study it might have been more sensible to consider age rather than either time since cirrhosis or time to infection as the primary timescale, at least for time to death.
Finally, whilst the approach might be novel for HPV patients, the 3-state approach is clearly widely used in other contexts, most specifically in HIV/AIDS studies. For instance the penalised likelihood approach of Joly and Commenges would be highly applicable.
The model consists of a simple unidirectional 3-state model. A parametric Weibull approach is taken, where the time to cirrhosis from infection has a standard Weibull distribution and the time from cirrhosis to death has a Weibull distribution where the scale parameter is a function of the time between infection and cirrhosis.
Unsurprisingly, they show that a full likelihood approach which takes into account the interval censoring is much less biased than an approach that ignores the problem of interval censoring.
A criticism of the model, which the authors acknowledge, is that the possibility of death before cirrhosis is not accommodated. Potentially, even under their current model there might also be cases where death occurs after cirrhosis but before diagnosis of cirrhosis - a scenario which isn't accommodated in the three cases listed in their likelihood development. The rate of increase of the hazard of cirrhosis from infection is observed to increase after 30 years since infection. It is not clear whether this is a real effect, whether it is due to a small number of people at risk or whether it is an artifact of not accommodating the possibility of death without cirrhosis. Given the long follow-up time in the study it might have been more sensible to consider age rather than either time since cirrhosis or time to infection as the primary timescale, at least for time to death.
Finally, whilst the approach might be novel for HPV patients, the 3-state approach is clearly widely used in other contexts, most specifically in HIV/AIDS studies. For instance the penalised likelihood approach of Joly and Commenges would be highly applicable.
Estimation of the Expected Number of Earthquake Occurrences Based on Semi-Markov Models
Irene Votsi, Nikolaos Limnios, George Tsaklidis and Eleftheria Papadimitriou have a new paper in Methodology and Computing in Applied Probability. In the paper major earthquakes in the Northern Aegean Sea are modelled by a semi-Markov process. Earthquakes of above 5.5 in magnitude are categorized into three groups, [5.5,5.6], [5.7,6.0] and [6.1,7.2] (7.2 being the highest record event in the dataset). The model assumes that probability the next earthquake is of a particular category depends only on the category of the current earthquake (embedded Markov chain), and given a particular transition i->j is to occur, the waiting times between events has some distribution f_{ij}(t). Hence the inter-event times will follow a mixture distribution dependent on i. Note that the process can renew in the same state (i.e. two earthquakes of similar magnitude can occur consecutively).
The dataset used is quite small, involving only 33 events.
The observed matrix of transitions is
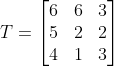
Clearly something of basic interest would be whether there is any evidence of dependence on the previous earthquake type. A simple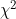
test gives 2.55 on 2 df suggesting no evidence against independence.
The authors instead proceed with a fully non-parametric method which uses the limited number of observations per transition type (i.e. between 1 & 6) to estimate the conditional staying time distributions. While a semi-Markov process of this type may well be appropriate for modelling earthquakes, the limited dataset available is insufficient to get usable estimates.
There are some odd features to the paper. Figure 3 in particular is puzzling as the 95% confidence intervals for the expected number of magnitude [6.1,7.2] earthquakes are clearly far too narrow. It also seems strange that there is essentially no mention of the flowgraph/saddlepoint approximation approach to analyzing semi-Markov processes of this nature.
The dataset used is quite small, involving only 33 events.
The observed matrix of transitions is
Clearly something of basic interest would be whether there is any evidence of dependence on the previous earthquake type. A simple
The authors instead proceed with a fully non-parametric method which uses the limited number of observations per transition type (i.e. between 1 & 6) to estimate the conditional staying time distributions. While a semi-Markov process of this type may well be appropriate for modelling earthquakes, the limited dataset available is insufficient to get usable estimates.
There are some odd features to the paper. Figure 3 in particular is puzzling as the 95% confidence intervals for the expected number of magnitude [6.1,7.2] earthquakes are clearly far too narrow. It also seems strange that there is essentially no mention of the flowgraph/saddlepoint approximation approach to analyzing semi-Markov processes of this nature.
Friday, 14 October 2011
Shape constrained nonparametric estimators of the baseline distribution in Cox proportional hazards model
Hendrik Lopuhaa and Gabriela Nane have a preprint on the Arxiv that considers estimators for the baseline hazard of the Cox proportional hazards model, subject to monotonicity constraints.
The basic idea is fairly straightforward. Using a standard NPMLE argument, the estimated hazard takes the form of a step function which is 0 before the first event time, and then piecewise constant between subsequent event times. For a fixed value of the regression coefficients,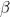, the baseline hazards can be found by performing a weighted pooled adjacent violators algorithm taking the weights as the (covariate corrected) time at risk in the next period and response as the empirical hazard in the next period i.e. 1/(time at risk) if the event was a failure and 0 if it was a censoring.
The authors argue that since Cox regression will give a consistent estimate of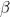 regardless of whether the baseline hazard is monotone or not, they propose a two-stage approach where one estimates beta using a standard Cox partial likelihood and then uses this value of 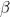to obtain the monotone baseline hazard. Obviously this estimator will have the same asymptotic properties as one based on maximizing the full likelihood jointly. Naively, a profile likelihood approach would seem possible since calculating the likelihood conditional on 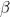is straightforward (though it is not clear whether it would be differentiable). Interestingly some quick simulations on Weibull data with shape>1 seem to suggest the full likelihood estimator of 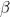(using the monotonicity constraint) is more biased and less efficient for small samples.
A substantial proportion of the paper is dedicated to obtaining the asymptotic properties of the estimators, which are non-standard and require empirical process theory. There is also some discussion of obtaining baseline hazards based on an increasing density constraint via analogous use of the Grennader estimator. Update: This paper has now been published in the Scandinavian Journal of Statistics.
The basic idea is fairly straightforward. Using a standard NPMLE argument, the estimated hazard takes the form of a step function which is 0 before the first event time, and then piecewise constant between subsequent event times. For a fixed value of the regression coefficients,
The authors argue that since Cox regression will give a consistent estimate of
A substantial proportion of the paper is dedicated to obtaining the asymptotic properties of the estimators, which are non-standard and require empirical process theory. There is also some discussion of obtaining baseline hazards based on an increasing density constraint via analogous use of the Grennader estimator. Update: This paper has now been published in the Scandinavian Journal of Statistics.
Thursday, 6 October 2011
A case-study in the clinical epidemiology of psoriatic arthritis: multistate models and causal arguments
Aidan O'Keeffe, Brian Tom and Vern Farewell have a new paper in Applied Statistics. They model data on the status of 28 individual hand joints in psoriatic arthitis patients. The damage to joints for a particular patient is expected to be correlated. Particular questions of interest are whether the damage process has 'symmetry', meaning if a specific joint in one hand is damaged does this increase the hazard of the corresponding joint in the other hand becoming damaged, and whether activity, meaning whether a joint is inflamed, causes the joint damage.
Two approaches to analysing the data are taken. In the first each pair of joints (from the left and right hands) is modelled by a 4 state model where the initial state is no damage to either joint, the terminal state is damage to both joints and progession to the terminal state may be through either a state representing damage only to the left joint or through a state representing damage only to the right joint. The correlation between joints within a patient is incorporated by allowing a common Gamma frailty which affects all transition intensities for all 14 pairs of joints. Symmetry can then be assessed by comparing the hazard of damage to the one joint with or without damage having occurred to the other joint. Under this approach, activity is incorporated only as a time dependent covariate. There are two limitations to this. Firstly, panel observation means that some assumption about the status of activity between clinic visits has to be made (e.g. it keeps the status observed at the last clinic visit until the current visit) and, from a causal inference perspective, activity is an internal time dependent covariate so treating it as fixed makes it harder to infer causality.
The second approach seeks to address these problems by jointly modelling activity and joint damage as linked stochastic processes. In this model each of the 28 joints is represented by a three-state model where the first two states represent presence and absence of activity for an undamaged joint, whilst state three represents joint damage. For this model, rather than explicitly fitting a random effects model, a GEE type approach is taken where the parameter point estimates are based on maximizing the likelihood assuming independence of the 28 joint processes, but standard errors are calculated using a sandwich estimator based on patient level clustering. This approach is valid provided the point estimates are consistent, which will be the case if the marginal processes are Markov. For instance if the transition intensities of type {ij} are linked via a random effect u such that} = u_{l}\lambda_{ij}^{(k)} "\lambda_{ij}^{(lk)} = u_{l}\lambda_{ij}^{(k)}")
.
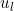The basic model considered is (conditionally) Markov. The authors attempt to relax this assumption by allowing the transition intensities to joint damage from the non-active state to additionally depend on a time dependent covariate indicating whether activity has ever been observed. Ideally the intensity should depend on whether the patient has ever been active rather than whether they have been observed to be active. This could be incorporated very straightforwardly by modelling the process as a 4 state model where state 1 represents never active, no damage, state 2 represents active, no damage, state 3 represents not currently active (but have been in the past) and state 4 represents damage. Clearly, we cannot always determine whether the current occupied state is 1 or 3 so the observed data would come from a simple hidden Markov model.
On a practical level, the authors fit the likelihood for the gamma random effects model by using the integrate function in R, for each patient's likelihood contribution for each likelihood evaluation in the (derivative-free) optimization. Presumably this is very slow. Using a simpler more explicit quadrature formulation would likely improve speed (at a very modest cost to accuracy) because the contributions for all patients for each quadrature point could be calculated at the same time and the overall likelihood contributions could then be calculated in the same operation. Alternatively, the likelihood for a single shared Gamma frailty is in fact available in closed form. This follows from arguments extending the results in the tracking model of Satten (Biometrics, 1999). Essentially, we can write every term in the conditional likelihood as some weighted sum of exponentials:
} "\sum_i w_i \exp{(-u_i t)}")
the product of these terms is then still in this form:
}. "\sum_k w^{*}_k \exp{(-u_k t^{*}_k)}.")
Calculating the marginal likelihood then just involves computing a series of Laplace transforms.
Provided the models are progressive, keeping track of the separate terms is feasible, although the presence of time dependent covariates makes this approach less attractive.
Two approaches to analysing the data are taken. In the first each pair of joints (from the left and right hands) is modelled by a 4 state model where the initial state is no damage to either joint, the terminal state is damage to both joints and progession to the terminal state may be through either a state representing damage only to the left joint or through a state representing damage only to the right joint. The correlation between joints within a patient is incorporated by allowing a common Gamma frailty which affects all transition intensities for all 14 pairs of joints. Symmetry can then be assessed by comparing the hazard of damage to the one joint with or without damage having occurred to the other joint. Under this approach, activity is incorporated only as a time dependent covariate. There are two limitations to this. Firstly, panel observation means that some assumption about the status of activity between clinic visits has to be made (e.g. it keeps the status observed at the last clinic visit until the current visit) and, from a causal inference perspective, activity is an internal time dependent covariate so treating it as fixed makes it harder to infer causality.
The second approach seeks to address these problems by jointly modelling activity and joint damage as linked stochastic processes. In this model each of the 28 joints is represented by a three-state model where the first two states represent presence and absence of activity for an undamaged joint, whilst state three represents joint damage. For this model, rather than explicitly fitting a random effects model, a GEE type approach is taken where the parameter point estimates are based on maximizing the likelihood assuming independence of the 28 joint processes, but standard errors are calculated using a sandwich estimator based on patient level clustering. This approach is valid provided the point estimates are consistent, which will be the case if the marginal processes are Markov. For instance if the transition intensities of type {ij} are linked via a random effect u such that
The basic model considered is (conditionally) Markov. The authors attempt to relax this assumption by allowing the transition intensities to joint damage from the non-active state to additionally depend on a time dependent covariate indicating whether activity has ever been observed. Ideally the intensity should depend on whether the patient has ever been active rather than whether they have been observed to be active. This could be incorporated very straightforwardly by modelling the process as a 4 state model where state 1 represents never active, no damage, state 2 represents active, no damage, state 3 represents not currently active (but have been in the past) and state 4 represents damage. Clearly, we cannot always determine whether the current occupied state is 1 or 3 so the observed data would come from a simple hidden Markov model.
On a practical level, the authors fit the likelihood for the gamma random effects model by using the integrate function in R, for each patient's likelihood contribution for each likelihood evaluation in the (derivative-free) optimization. Presumably this is very slow. Using a simpler more explicit quadrature formulation would likely improve speed (at a very modest cost to accuracy) because the contributions for all patients for each quadrature point could be calculated at the same time and the overall likelihood contributions could then be calculated in the same operation. Alternatively, the likelihood for a single shared Gamma frailty is in fact available in closed form. This follows from arguments extending the results in the tracking model of Satten (Biometrics, 1999). Essentially, we can write every term in the conditional likelihood as some weighted sum of exponentials:
the product of these terms is then still in this form:
Calculating the marginal likelihood then just involves computing a series of Laplace transforms.
Provided the models are progressive, keeping track of the separate terms is feasible, although the presence of time dependent covariates makes this approach less attractive.
Tuesday, 4 October 2011
A Bayesian Simulation Approach to Inference on a Multi-State Latent Facotr Intensity Model
Chew Lian Chua, G.C. Lim and Penelope Smith have a new paper in the Australian and New Zealand Journal of Statistics. This models the trajectory of credit ratings of companies. While there are 26 possible rating classes, these are grouped to the 4 broad classes: A,B,C,D, Movement between any two classes is deemed possible resulting in 12 possible transition types. The authors develop methods for fitting what is termed a multi-state latent factor intensity model. This is essentially a multi-state model with a shared random effect that affects all the transition intensities, but the random effect is allowed to evolve in time. For instance, the authors assume the random effect is an AR(1) process.
There seems to be some confusion in the formulation of the model as to whether the process is in continuous or discrete time: The process is expressed in terms of intensities which are "informally" defined as = \lim_{t_{i} - t_{i-1} \downarrow 0} \frac{P(N_{sk}(t_i) - N_{sk}(t_{i-1}) > 0 | \mathcal{F}_{t_{i}-1})}{t_i - t_{i-1}} "\lambda_{sk}(t_i) = \lim_{t_{i} - t_{i-1} \downarrow 0} \frac{P(N_{sk}(t_i) - N_{sk}(t_{i-1}) > 0 | \mathcal{F}_{t_{i}-1})}{t_i - t_{i-1}}")
where "\inline N_{sk}(t)")
is a counting process describing the number of s to k transitions that have occurred to time t and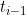 
is the ith observation time. But if the time between observations 
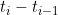were variable, the AR(1) formulation (which takes no account of this) would not seem sensible.
Nevertheless the idea of having a random effect that can vary temporally within a multi-state model (proposed by Koopman et al) is interesting, though obviously presents various computational challenges which is the main focus of Chua, Lim and Smith's paper.
There seems to be some confusion in the formulation of the model as to whether the process is in continuous or discrete time: The process is expressed in terms of intensities which are "informally" defined as
where
Nevertheless the idea of having a random effect that can vary temporally within a multi-state model (proposed by Koopman et al) is interesting, though obviously presents various computational challenges which is the main focus of Chua, Lim and Smith's paper.
Subscribe to:
Posts (Atom)