Hendrik Lopuhaa and Gabriela Nane have a
preprint on the Arxiv that considers estimators for the baseline hazard of the Cox proportional hazards model, subject to monotonicity constraints.
The basic idea is fairly straightforward. Using a standard NPMLE argument, the estimated hazard takes the form of a step function which is 0 before the first event time, and then piecewise constant between subsequent event times. For a fixed value of the regression coefficients,
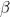
, the baseline hazards can be found by performing a weighted pooled adjacent violators algorithm taking the weights as the (covariate corrected) time at risk in the next period and response as the empirical hazard in the next period i.e. 1/(time at risk) if the event was a failure and 0 if it was a censoring.
The authors argue that since Cox regression will give a consistent estimate of
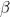
regardless of whether the baseline hazard is monotone or not, they propose a two-stage approach where one estimates beta using a standard Cox partial likelihood and then uses this value of
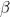
to obtain the monotone baseline hazard. Obviously this estimator will have the same asymptotic properties as one based on maximizing the full likelihood jointly. Naively, a profile likelihood approach would seem possible since calculating the likelihood conditional on
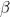
is straightforward (though it is not clear whether it would be differentiable). Interestingly some quick simulations on Weibull data with shape>1 seem to suggest the full likelihood estimator of
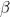
(using the monotonicity constraint) is more biased and less efficient for small samples.
A substantial proportion of the paper is dedicated to obtaining the asymptotic properties of the estimators, which are non-standard and require empirical process theory. There is also some discussion of obtaining baseline hazards based on an increasing density constraint via analogous use of the Grennader estimator.
Update: This paper has now been
published in the Scandinavian Journal of Statistics.
No comments:
Post a Comment