Likelihood based inference for current status data on a grid

Runlong Tang, Moulinath Banerjee and Michael Kosorok have a new paper in the Annals of Statistics. This considers the problem of non-parametric inference for current status data when the set of observation times is a grid of points such that multiple individuals can have the same observation time. This is distinct from the scenario usually considered in the literature where the observation times are generated from a continuous distribution, such that the unique number of observation times, K, is equal to the number of subjects, n. 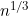In this case, non-standard (Chernoff) asymptotics with a convergence rate of applies. A straightforward alternative situation is where the total number of possible observation times has a fixed K. 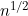Here, standard Normal asymptotics apply as n tends to infinity (though n may need to be much larger than K for approximations based on this to have much practical validity).

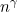
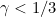
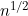
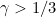
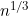
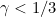
The authors consider a middle situation where K is allowed to increase with n at rate . They show that provided , standard asymptotics apply, whereas when , the asymptotics of the continuous observation scheme prevail. Essentially for , the NPMLE at each grid time point tends to its naive estimator (i.e. the proportion of failures at that time among those subjects observed there) and the isotonization has no influence. 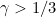Whereas for there will continue to be observation times sufficiently "close" but distinct such that the isotonization will have an effect. 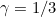A special boundary case applies when , with an asymptotic distribution depending on c where c determines the spacing between grid points via .

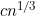
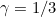
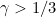
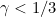
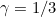
Having established these facts, the authors then develop an adaptive inference method for estimating F at a fixed point. They suggest a simple estimator for c, based on the assumption that . The estimator has the property that c will tend to 0 if and tend to infinity if . Concurrently, it can be shown that the limiting distribution for the case tends to the standard normal distribution as c tends to infinity and tends to the Chernoff distribution when c goes to 0. 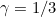As a consequence, constructing confidence intervals by assuming the asymptotics but with c estimated, will give valid asymptotic confidence intervals regardless of the true value of .

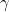
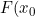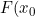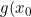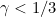
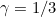
There are some practical difficulties with the approach as the error distribution of the NPMLE of depends both on and the sampling distribution density as well as c. Moreover, whereas for , there is scaling invariance such that one can express the errors in terms of a function of an indexable distribution (i.e. the Chernoff distribution). The boundary distribution for does not admit such scaling so would require bespoke simulations to establish for each case.