A Bayesian Simulation Approach to Inference on a Multi-State Latent Facotr Intensity Model

Chew Lian Chua, G.C. Lim and Penelope Smith have a new paper in the Australian and New Zealand Journal of Statistics. This models the trajectory of credit ratings of companies. While there are 26 possible rating classes, these are grouped to the 4 broad classes: A,B,C,D, Movement between any two classes is deemed possible resulting in 12 possible transition types. The authors develop methods for fitting what is termed a multi-state latent factor intensity model. This is essentially a multi-state model with a shared random effect that affects all the transition intensities, but the random effect is allowed to evolve in time. For instance, the authors assume the random effect is an AR(1) process.

There seems to be some confusion in the formulation of the model as to whether the process is in continuous or discrete time: The process is expressed in terms of intensities which are "informally" defined as
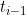
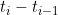
where is a counting process describing the number of s to k transitions that have occurred to time t and is the ith observation time. But if the time between observations were variable, the AR(1) formulation (which takes no account of this) would not seem sensible.

Nevertheless the idea of having a random effect that can vary temporally within a multi-state model (proposed by Koopman et al) is interesting, though obviously presents various computational challenges which is the main focus of Chua, Lim and Smith's paper.