Arnold Mitnitski, Nader Fallah, Charmaine Dean and Kenneth Rockwood have a new
paper in Statistical Methods in Medical Research. The paper develops a model to describe the trajectory of cognitive function test data. The responses are test scores out of 100, but the authors choose to group responses in 12 states. Additionally subjects may die before the following assessment. Assessments occur at (roughly) equally spaced intervals so a discrete-time model is adopted. Essentially the data are then ordinal longitudinal data.
The novel aspect of the model is to assume that, conditional on survival between time j-1 and j, the state at time j follows a truncated Poisson distribution on
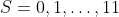
, with the mean of the Poisson distribution taken as a linear function of the state at time j and covariates (including age and/or time since baseline measurement). A separate logistic regression model is applied to the deaths. This avoids having to pretend the data are continuous as one might if a linear mixed model were used, and also avoids there being a very large number of unknown parameters, as there would be if a general discrete-time Markov model were applied. However, the truncated Poisson distribution model makes strong assumptions about the conditional distribution of the states, which may or may not be well supported by the data. The authors note that the model fits better if 12 states are used rather than 16. Whether accommodating the proposed model should be a criterion for choosing the number of states to use in the model is questionable.
It is not clear a multi-state model is particularly appropriate for modelling a response with such a large number of responses. It might be better to follow a latent trait approach where
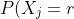 = P(x_r < \theta_j \leq x_{r+1}))
for some Normally distributed latent variable
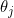
that evolves with time deterministically with the addition of stationary Gaussian noise (not necessarily independent), where the
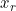
are boundary values to be estimated. Similarly existing approaches to modelling MMSE based on a much simpler classification into cognitive-normal and cognitive-impaired with the possibility of misclassification considered (see e.g.
Van den Hout and Matthews) are likely to give more meaningful results, even if data from raw MMSE scores is sacrificed.
No comments:
Post a Comment