Jeremy Sumner, Jesus Fernandez-Sanchez and Peter Jarvis have a
paper recently made available at thehttp://www.blogger.com/img/blank.gif Arxiv. The paper is theoretical in nature but gives an interesting application of group theory to Markov models.
The practical problem addressed is determining the conditions under which a non homogeneous continuous time Markov model can be represented by a "time averaged" homogeneous Markov model, i.e. what constraints are required to ensure a rate matrix
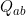
exists such that
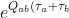} = e^{Q_a \tau_a } e^{Q_b \tau_b})
for rate matrices
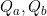
. This has application for phylogenetic methods, where typically a single rate matrix is fitted to an evolutionary history. However, rates may in fact change over time. The question is then under what conditions could the single rate still be in some sense valid in summarising the time averaged process.
The authors show that the model for Q must be a Lie algebra. They also give the possible model forms for three and four state models under symmetry constraints.
Update: This paper has now been
published in the Journal of Theoretical Biology.
1 comment:
Post a Comment