Comparison of prediction models for competing risks with time-dependent covariates

Giuliana Cortese, Thomas Gerds and Per Kragh Andersen have a new paper available as a University of Copenhagen Department of Biostatistics technical report. The paper concerns the development of models for prediction for competing risks in the presence of internal time dependent covariates. This is a follow-up to Cortese and Andersen's 2010 Biometrical Journal paper. 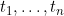Like the previous paper, the authors compare a multi-state modelling approach that explicitly models the progression of the (categorical) time dependent covariate and its effect on the cause specific hazards, and a landmarking approach that sets (arbitrarily chosen) time points and performs separate regressions to estimate the hazards for conditional on the value of the time dependent covariate at time . 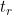The authors consider two modelling approaches under landmarking, one based on Cox regression of cause-specific hazards and the other based on Fine-Gray subdistribution hazards.

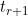
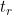
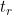
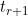
They compare the predictive ability of the models to predict the outcome by landmark given data up to . This is assessed by using a time dependent Brier score (Gerds & Schumacher, 2006). Rather than use inverse probability weighting, the authors instead use a pseudo-value to estimate outcomes when a subject is lost to follow-up between and . The authors perform the comparison using a bone marrow transplant study where the competing events are relapse and death, and the internal time dependent covariate is the development of Graft versus Host Disease (GvHD). The predictive abilities are estimated via cross-validation involving randomly choosing 2/3 of patients as training data and using the remainder as test data, repeating the process 100 times. For the data considered the three methods performed equally well in terms of prediction error. As might be expected, there was significantly improved predictive ability of these models compared to one that ignored GvHD (i.e. only considered baseline time constant covariates).

As the authors note, there are advantages and disadvantages to both approaches. The multi-state modelling approach requires modelling of the covariate process (e.g. Markov or semi-Markov assumptions and proportional hazard assumptions on the effect of baseline covariates on transition rates through covariate states) and requires a categorical covariate. Landmarking can accommodate continuous covariates but relies on an arbitrary set of landmark times and requires fitting regressions at each landmark. The extra modelling required for the multi-state approach may either be a blessing, in terms of having the potential to give a greater insight into the whole process, or a curse (questions of robustness to incorrect modelling assumptions).