Alexia Savignoni, David Hajage, Pascale Tubert-Bitter
and Yann De Ryckea have a new
paper in Statistics in Medicine. This considers developing illness-death type models to investigate the effect of pregnancy on the risk of recurrence of cancer amongst breast cancer patients. The authors give a fairly clear account of different potential models with particular reference to the hazard ratio
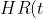 = \frac{\lambda_{23}(t,\mathbf{z})}{\lambda_{13}(t,\mathbf{z})})
The simplest model to consider is a Cox model with a single time dependent covariate representing pregnancy, here
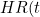 = \exp(\delta))
. This can be extended by assuming non-proportional hazards which effectively makes the effect time dependent i.e.
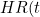 = \exp(\delta(t)))
.
Alternatively, an unrestricted Cox-Markov model could be fitted with separate covariate effects and non-parametric hazards from each pregnancy state, yielding:
![HR(t) = \exp[(\beta_{23} - \beta_{13})^{T} \mathbf{z}] \frac{\lambda_{23}(t)}{\lambda_{13}(t)}](http://latex.codecogs.com/gif.latex?HR(t) = \exp[(\beta_{23} - \beta_{13})^{T} \mathbf{z}] \frac{\lambda_{23}(t)}{\lambda_{13}(t)})
This model can be restricted by allowing a shared baseline hazard for
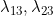
giving either
![\inline HR(t) = \exp{\[(\beta_{23} - \beta_{13})^{T} \mathbf{z} + \delta]}](http://latex.codecogs.com/gif.latex?\inline HR(t) = \exp{\[(\beta_{23} - \beta_{13})^{T} \mathbf{z} + \delta]})
under a Cox model with a fixed effect or
![\inline HR(t) = \exp{\[(\beta_{23} - \beta_{13})^{T} \mathbf{z} + \delta(t)]}](http://latex.codecogs.com/gif.latex?\inline HR(t) = \exp{\[(\beta_{23} - \beta_{13})^{T} \mathbf{z} + \delta(t)]})
for a time dependent effect.
If we were only interested in
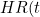)
and any of these models seems feasible, there doesn't actual seem that much point in formulating the model as an illness-death model. Note that the transition rate
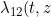)
does not feature in any of the above equations but would be estimated in the illness-death model. The above models can be fitted by a Cox model with a time dependent covariate (representing pregnancy) that has an interaction with the time fixed covariates.
The real power of a multi-state model approach would only become apparent if we were interested in the overall survival for different covariates, treating pregnancy as a random event.
The time dependent effects
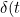)
are represented simply via a piecewise constant time indicator in the model. The authors do acknowledge that a spline model would have been better. The other issue that could have been considered is whether the effect of pregnancy depends on time since initiation of pregnancy (i.e. a semi-Markov effect). An issue in their data example is that pregnancy is only determined via a successful birth meaning there may be some truncation in the sample (through births prevented due to relapse/death).
No comments:
Post a Comment