Jin-Jian Hsieh and Yu-Ting Huang have a new
paper in Lifetime Data Analysis. This develops a conditional likelihood approach to fitting regression models with time-dependent covariate effects for the time to the non-terminal event in a semi-competing risks model. In line with some other recent treatments of competing and semi-competing risks (e.g.
Chen, 2012), the authors use a copula to model the dependence between the times to the competing events. The authors express the data at a particular time point t in terms of indicator functions
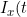 = I(X > t))
and
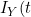 = I(Y > t))
where
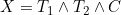
refers to the time of the non-terminal event (or its censoring time) and
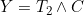
refers to the terminal event (or its censoring time). The authors show that the likelihood for the data at t can be expressed in terms of a term relating solely to the
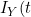)
, which depends only on the covariate function for the terminal event, and a term based on
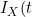 | I_{Y}(t))
which contains all the information on the covariate function of interest for the non-terminal event. They therefore propose to base estimation on maximization on a conditional likelihood based on this conditional term only. The authors allow the copula itself to have a time specific copula dependence parameter. Solving the score function at a particular value of t gives consistent estimates of the parameters so the authors adopt a "working independence" model to obtain estimates across the sequence of times. The resulting estimates are step-functions that only change at observed event times.
Presumably allowing the copula dependence to be time varying could lead to situations where, for instance,
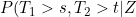)
, is not a decreasing function in s for fixed t and Z. So whilst allowing the copula dependence to vary is convenient computationally, it is unclear how the model would be interpreted if the dependence parameter was estimated to vary considerably (perhaps that the chosen copula family were inappropriate?).
As usual, with these models that ascribe an explicit dependence structure between the competing event times, one has to ask whether the marginal distribution of the non-terminal event is what we are really interested in and whether we should not instead be sticking to observable quantities like the cumulative incidence function?
No comments:
Post a Comment