Modeling Left-truncated and right-censored survival data with longitudinal covariates

Yu-Ru Su and Jane-Ling Wang have a new paper in the Annals of Statistics. This considers the problem of modelling survival data in the presence of intermittently observed time varying covariates when the survival times are both left truncated as well as right-censored. They consider a joint model which involves assuming there exists a random effect which influences both the longitudinal covariate values (which are assumed to be a function of the random effects plus Gaussian error) and the survival hazard. Considerably work has been done in this area in cases where the survival times are merely right-censored (e.g. Song, Davidian and Tsiatis, Biometrics 2002). The authors show that the addition of left-truncation complicates inference quite considerably; firstly because the parameters affecting the longitudinal component may not be identifiable and secondly because the score equations for the regression and baseline hazard parameters become much more complicated than in the right-censoring case. To alleviate this problem, the authors propose to use a modified likelihood rather than either the full or conditional likelihood. The full likelihood can be expressed in terms of an integral over the conditional distribution of the random effect, given the event time occurred after the truncation time. The proposed modification is to instead integrate over the unconditional random effect distribution. Heuristically this is justified by noting that
and
where 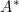is the random effect. The authors also show inference based on this modified likelihood gives consistent and asymptotically efficient estimators of the regression parameters and the baseline survival hazard.

An EM algorithm to obtain the MMLE is outlined, in which the E-step involves a multi-dimensional integral which the authors evaluate through Monte Carlo approximation. The implementation of the EM algorithm is simplified if the random effect is assumed to have a multivariate Normal distribution.