An EM algorithm to obtain the MMLE is outlined, in which the E-step involves a multi-dimensional integral which the authors evaluate through Monte Carlo approximation. The implementation of the EM algorithm is simplified if the random effect is assumed to have a multivariate Normal distribution.
Tuesday, 27 March 2012
Modeling Left-truncated and right-censored survival data with longitudinal covariates
Yu-Ru Su and Jane-Ling Wang have a new paper in the Annals of Statistics. This considers the problem of modelling survival data in the presence of intermittently observed time varying covariates when the survival times are both left truncated as well as right-censored. They consider a joint model which involves assuming there exists a random effect which influences both the longitudinal covariate values (which are assumed to be a function of the random effects plus Gaussian error) and the survival hazard. Considerably work has been done in this area in cases where the survival times are merely right-censored (e.g. Song, Davidian and Tsiatis, Biometrics 2002). The authors show that the addition of left-truncation complicates inference quite considerably; firstly because the parameters affecting the longitudinal component may not be identifiable and secondly because the score equations for the regression and baseline hazard parameters become much more complicated than in the right-censoring case. To alleviate this problem, the authors propose to use a modified likelihood rather than either the full or conditional likelihood. The full likelihood can be expressed in terms of an integral over the conditional distribution of the random effect, given the event time occurred after the truncation time. The proposed modification is to instead integrate over the unconditional random effect distribution. Heuristically this is justified by noting that
 = f_{A^{*}}(a)S_{Y}(t|A^{*}=a)/S_{Y}(t)) and
and
/S_{Y}(t) \right) = 1, \forall t \geq 0) where
where 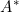 is the random effect. The authors also show inference based on this modified likelihood gives consistent and asymptotically efficient estimators of the regression parameters and the baseline survival hazard.
is the random effect. The authors also show inference based on this modified likelihood gives consistent and asymptotically efficient estimators of the regression parameters and the baseline survival hazard.
An EM algorithm to obtain the MMLE is outlined, in which the E-step involves a multi-dimensional integral which the authors evaluate through Monte Carlo approximation. The implementation of the EM algorithm is simplified if the random effect is assumed to have a multivariate Normal distribution.
An EM algorithm to obtain the MMLE is outlined, in which the E-step involves a multi-dimensional integral which the authors evaluate through Monte Carlo approximation. The implementation of the EM algorithm is simplified if the random effect is assumed to have a multivariate Normal distribution.
Monday, 26 March 2012
A note on the decomposition of number of life years lost according to causes of death
Per Kragh Andersen has a new paper available as a Department of Biostatistics, Copenhagen Research Report. He shows that the integral of the cumulative incidence function of a particular risk has an interpretation as the expected number of life years lost due to this cause, i.e.
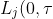 = \int_{0}^{\tau} F_j(t) dt = E(\tau - T_{(j)} \wedge \tau))
It is argued that this is a more appropriate quantification of the effect of a cause-of-death than using a hypothetical estimate of life expectancy without a particular cause of death, which is reliant on an (untestable) assumption of independent competing risks.
Regression models based around expected "life years lost" are proposed using the pseudo-observations method.
It is argued that this is a more appropriate quantification of the effect of a cause-of-death than using a hypothetical estimate of life expectancy without a particular cause of death, which is reliant on an (untestable) assumption of independent competing risks.
Regression models based around expected "life years lost" are proposed using the pseudo-observations method.
Wednesday, 14 March 2012
Regression analysis based on conditional likelihood approach under semi-competing risks data
Jin-Jian Hsieh and Yu-Ting Huang have a new paper in Lifetime Data Analysis. This develops a conditional likelihood approach to fitting regression models with time-dependent covariate effects for the time to the non-terminal event in a semi-competing risks model. In line with some other recent treatments of competing and semi-competing risks (e.g. Chen, 2012), the authors use a copula to model the dependence between the times to the competing events. The authors express the data at a particular time point t in terms of indicator functions
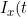 = I(X > t)) and
and 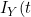 = I(Y > t)) where
where 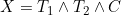 refers to the time of the non-terminal event (or its censoring time) and
refers to the time of the non-terminal event (or its censoring time) and 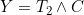 refers to the terminal event (or its censoring time). The authors show that the likelihood for the data at t can be expressed in terms of a term relating solely to the
refers to the terminal event (or its censoring time). The authors show that the likelihood for the data at t can be expressed in terms of a term relating solely to the 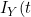) , which depends only on the covariate function for the terminal event, and a term based on
, which depends only on the covariate function for the terminal event, and a term based on 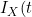 | I_{Y}(t)) which contains all the information on the covariate function of interest for the non-terminal event. They therefore propose to base estimation on maximization on a conditional likelihood based on this conditional term only. The authors allow the copula itself to have a time specific copula dependence parameter. Solving the score function at a particular value of t gives consistent estimates of the parameters so the authors adopt a "working independence" model to obtain estimates across the sequence of times. The resulting estimates are step-functions that only change at observed event times.
which contains all the information on the covariate function of interest for the non-terminal event. They therefore propose to base estimation on maximization on a conditional likelihood based on this conditional term only. The authors allow the copula itself to have a time specific copula dependence parameter. Solving the score function at a particular value of t gives consistent estimates of the parameters so the authors adopt a "working independence" model to obtain estimates across the sequence of times. The resulting estimates are step-functions that only change at observed event times.
Presumably allowing the copula dependence to be time varying could lead to situations where, for instance,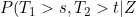) , is not a decreasing function in s for fixed t and Z. So whilst allowing the copula dependence to vary is convenient computationally, it is unclear how the model would be interpreted if the dependence parameter was estimated to vary considerably (perhaps that the chosen copula family were inappropriate?).
, is not a decreasing function in s for fixed t and Z. So whilst allowing the copula dependence to vary is convenient computationally, it is unclear how the model would be interpreted if the dependence parameter was estimated to vary considerably (perhaps that the chosen copula family were inappropriate?).
As usual, with these models that ascribe an explicit dependence structure between the competing event times, one has to ask whether the marginal distribution of the non-terminal event is what we are really interested in and whether we should not instead be sticking to observable quantities like the cumulative incidence function?
Presumably allowing the copula dependence to be time varying could lead to situations where, for instance,
As usual, with these models that ascribe an explicit dependence structure between the competing event times, one has to ask whether the marginal distribution of the non-terminal event is what we are really interested in and whether we should not instead be sticking to observable quantities like the cumulative incidence function?
Friday, 9 March 2012
Estimating Discrete Markov Models From Various Incomplete Data Schemes
Alberto Pasanisi, Shuai Fu and Nicolas Bousquet have a new paper in Computational Statistics & Data Analysis. This considers approaches to Bayesian inference for time-homogeneous discrete-time Markov models under incomplete observation. Firstly, they consider where there are missing observations in a sequence of states (considering different missingness assumptions). Secondly, they consider the case of aggregate data where all that is known is the number of subjects in each state at each time. A Bayesian approach is adopted throughout, which the authors claim is the most convenient in this situation.
The part involving incomplete data follows similar ground to Deltour et al (Biometrics, 1999). The problem only becomes non-trivial if the missingness mechanism is non-ignorable.
The treatment of aggregate data is incorrect as the authors state the likelihood as being the product of independent multinomial random variables with probabilities corresponding to the probability of being in a state at time t given the initial state distribution at time 0. As a result they claim the likelihood is proportional to the case of current status data where each subject or unit is only observed once. The reason that likelihood-based inference for aggregate data is so difficult is that we observe all units multiple times but don't know number or nature of the transitions that occurred. Hence, the full likelihood would require summing over all possible transitions consistent with the aggregate counts. Kalbfleisch and Lawless (Canadian Journal of Statistics, 1984) derived the mean and covariance of the aggregated counts across times to establish a least-squares estimation procedure. Pasanisi et al's procedure is only relevant when the data consist of a series of independent cross-sectional surveys at different time points all assumed to come from different units. An MCMC or simulation based approach would be necessary to compute the exact likelihood or posterior distribution in the true aggregate data case, which the authors did not pursue. However, the gain in efficiency compared to the least-squares approach is probably not worth the trouble except for very small counts. Crowder and Stephens (2011) pursued an approach based on matching the coefficients of the probability generating function of the aggregate counts.
The part involving incomplete data follows similar ground to Deltour et al (Biometrics, 1999). The problem only becomes non-trivial if the missingness mechanism is non-ignorable.
The treatment of aggregate data is incorrect as the authors state the likelihood as being the product of independent multinomial random variables with probabilities corresponding to the probability of being in a state at time t given the initial state distribution at time 0. As a result they claim the likelihood is proportional to the case of current status data where each subject or unit is only observed once. The reason that likelihood-based inference for aggregate data is so difficult is that we observe all units multiple times but don't know number or nature of the transitions that occurred. Hence, the full likelihood would require summing over all possible transitions consistent with the aggregate counts. Kalbfleisch and Lawless (Canadian Journal of Statistics, 1984) derived the mean and covariance of the aggregated counts across times to establish a least-squares estimation procedure. Pasanisi et al's procedure is only relevant when the data consist of a series of independent cross-sectional surveys at different time points all assumed to come from different units. An MCMC or simulation based approach would be necessary to compute the exact likelihood or posterior distribution in the true aggregate data case, which the authors did not pursue. However, the gain in efficiency compared to the least-squares approach is probably not worth the trouble except for very small counts. Crowder and Stephens (2011) pursued an approach based on matching the coefficients of the probability generating function of the aggregate counts.
Subscribe to:
Comments (Atom)