Mitchell, Hudgens, King, Cu-Uvin, Lo, Rompalo, Sobel and Smith have a new
paper in Statistics in Medicine. This considers a non-parametric estimator for a 2-state discrete-time semi-Markov process. Following
Kang and Lagakos who assume one of the two states (e.g. state 0) is Markov, the process can be characterised by
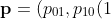,p_{10}(2),\ldots,p_{10}(n_t - 1),p_{1+}(n_t)))
where
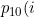)
is the probability of making a transition from 1 to 0 given i time units spent in state 1,
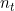
is the maximum length of state sequence observable in the data and
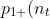 = 1 - \sum_{i=1}^{n_t - 1} p_{10}(i).)
Extensions to the model, allowing
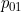
to depend on time in state and to allow an additional disease-free state
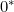
corresponding to disease-free with no past disease, are also proposed. Missing observations can be dealt with by summing over all possible observed states at the missing times. Estimation of
is by maximum likelihood. An acknowledged limitation is the inability to cope with the case of unknown initiation times if either the sojourn distribution of state 0 is non-geometric or observation can start in the disease state.
Of particular interest to the authors is an estimate of 'persistence' of the disease state. This is defined as spending j time units in the disease state, counting single disease free (negative) observations surrounded by positive observations as time spent in the disease. The probability of persistence is just a function of the transition probabilities
and so readily estimable.
The authors claim that their discrete time model doesn't not require a "guarantee time" unlike
Kang and Lagakos. This is obviously ridiculous, the discrete time model requires a guarantee time of 1 time unit for all transitions! While adopting a discrete time model simplifies the problem of inference to something quite trivial, one has to question how realistic it is to model something that is clearly a continuous time process as discrete time.
Bachetti et al's more general approach is along similar lines. Similarly, while the estimation is nominally non-parametric, the discrete time assumption is in many respects more severe than, say, constraining sojourn distributions to be Weibull distributed.
The clinical definition of persistence which makes the assumption that a negative observation between two positive observations counts as a positive is easily accommodated for via the discrete time model. However, a more satisfactory approach would be to adopt a more formal definition, based in continuous time, e.g. persistence if disease free period is less than say 6 months. This would have parallels with the approach taken by
Mandel (2010) in defining a hitting time in terms of having a sojourn of more than some length in the disease state.
Farewell and Su also dealt with a similar problem but their approach seems to be best avoided.