Semiparametric transformation models for current status data with informative censoring

Chyong-Mei Chen, Tai-Fang Lu, Man-Hua Chen and Chao-Min Hsu have a new paper in Biometrical Journal. In common with the recent paper by Wang et al, this considers the estimation of current status data under informative censoring. Here, rather than using a copula to describe the dependence between censoring and failure time distributions, a shared frailty is assumed between the censoring intensity and the failure intensity. The frailty is assumed to be log-normal such that and Covariate effects are also allowed for via a general class of transformation models. For estimation, the authors approximate the semi-parametric maximum likelihood estimate by assuming that the conditional intensities, for the censoring and failure events, are piecewise constant functions with an arbitrarily chosen set of change points. Since maximization of the likelihood requires estimation of a large number of unknown parameters and integration of the frailty distribution, the authors propose an EM algorithm. The method attempts to non-parametrically estimate the failure and censoring time distributions and also the variance of the frailty term. While the assumed dependence between T & C is reasonably restrictive, ie. the frailty could feasible have appeared as within the intensity for C allowing other types of dependence. Nevertheless, even with the restrictions it is not clear how the overall model is identifiable. We can only observe where 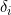is an indicator for whether the failure has occurred by censoring time 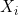. Log-normal frailties are not particularly nice computationally, whereas a Gamma frailty would allow some tractability. In the case of a shared frailty it can be shown that the marginal distribution of censoring times is and the conditional probability of a failure by time X is given by The problem is that we can vary the value of v and find new cumulative intensity functions which will result in the same distribution functions. The addition of covariates via a particular model facilitates some degree of identifiability but, in a similar way to frailty terms in univariate Cox-proportional hazard models, this could just as easily be describing misspecification of the covariate model rather than true dependence.