Bootstrap confidence bands for sojourn distributions in multistate semi-Markov models with right censoring

Ronald Butler and Douglas Bronson have a new paper in Biometrika. This develops approaches to non-parametric estimation of survival or hitting time distributions in multi-state semi-Markov models with particular emphasis on cases where (multiple) backward transitions are possible. The paper is an extension of the authors' previous JRSS B paper. Here the methodology additionally allows for right-censored observations.

The key property used throughout is that, under a semi-Markov model, the data can be partitioned into separate independent sets relating to the sojourn and destinations for each state.
A straightforward, but computationally intensive, approach to finding bootstrap confidence bands for the survival distribution of a semi-Markov process involves a nested re-sampling scheme, first sampling with replacement from the set of pairs of sojourn times and destination states for each state in the network, and for each set of data simulating a large number of walks through the network (starting from the initial state and ending at the designated 'hitting' state) from the empirical distributions implied from the first layer of re-sampling. An alternative, faster approach proposed involves replacing the inner step of the bootstrap with a step which computes saddlepoint approximations of the empirical sojourn distributions and then using flowgraph techniques to find the implied hitting time distributions. A drawback of both approaches is that they require all the mass of the sojourn distributions to be allocated. Hence, in the presence of right-censoring some convention for the mass at the tail of the distribution must be made. Here, the convention of "redistribute-to-the-right" is used, which effectively re-weights the probability mass of all the observed survival times so that it sums to 1. On the face of it this seems a rash assumption. However, right-censoring in the sample only occurs at the end of a sequence of sojourns in several states. As such, in most cases where this technique would be used, the censoring in any particular state is likely to be quite light, even if the overall observed hitting times are heavily censored. Alternative conventions on the probability mass (for instance assuming a constant hazard beyond some point) could be made, but in all cases would be arbitrary, but hopefully would have little impact on the overall estimates.

Unlike non-parametric estimates under a Markov assumption, for which the overall survival distribution will essentially equal the overall Kaplan-Meier estimate, with increasing uncertainty as time increases, under a (homogeneous) semi-Markov assumption the estimated hazard tends to a constant limit and can hence be estimated to a relatively large degree of precision at arbitrarily high times.

A semi-Markov model for stroke with piecewise-constant hazards in the presence of left, right and interval censoring

Venediktos Kapetanakis, Fiona Matthews and Ardo van den Hout have a new paper in Statistics in Medicine. This develops a progressive three-state illness-death model for strokes with interval-censored data. The proposed model is a time non-homogeneous Markov model. The main approach to computation is to assume a continuous effect of age (time) on transition intensities but to use a piecewise constant approximation to actually fit it. The intensity to death from the stroke state additionally depends on the time since entry into the state (i.e. age at stroke) and since the exact time is typically unknown, it is necessary to numerically integrate over the possible range of transition times (here using Simpson's rule).

The data include subjects whose time to stroke is left-censored because they have already suffered a stroke before the baseline measurement. The authors state that they cannot integrate out the unknown time of stroke because the left-interval (i.e. the last age at which the subject is known to have been healthy) is unknown. They then proceed to propose a seemingly unnecessary ad-hoc EM-type approach based on estimating the stroke age for these individuals, which requires the arbitrary choice of an age at which it can be assumed the subject was stroke free. However, surely if we can assume a , we can just use as the lower limit in the integral for the likelihood?

The real issue seems to be that all subjects are effectively left-truncated at the time of entry into the study (in the sense that they are only sampled due to not having died before their current age). For subjects who are healthy at baseline this left-truncation is accounted for by just integrating the hazards of transition out of state 1 from their age at baseline rather than age 0. For subjects who have already had a stroke things are more complicated because the fact they have survived provides information on the timing of the stroke (e.g. if stroke increases hazard of death, the fact they have survived implies the stroke occurred sooner than one would assume if no information on survival were known). Essentially the correct likelihood is conditional on survival to time and so the unconditional probability of the observed data needs to be divided through by the unconditional probability of survival to time . For instance, in their notation, a subject in state 2 at baseline censored at time should have likelihood contribution: The authors claim that their convoluted EM-approach has "bypassed the problem of left truncation". In reality, they have explicitly corrected for left-truncation (because the expected transition time is conditional on being in state 2 at baseline) but in a way that is seemingly much more computationally demanding than directly computing the left-truncated likelihood would be.

Absolute risk regression for competing risks: interpretation, link functions, and prediction

Thomas Gerds, Thomas Scheike and Per Andersen have a new paper in Statistics in Medicine. To a certain extent this is a review paper and considers models for direct regression on the cumulative incidence function for competing risks data. Specifically models of the form where is a known link function and is the cumulative incidence function for event 1 given covariates X. The Fine-Gray model is a special case of this class of models, where a complementary log-log link is adopted. Approaches to estimation based on inverse probability of censoring weights and jackknife based pseudo-observations are considered. Model comparison based on predictive accuracy as measured through Brier score and model diagnostics based on extended models allowing time dependent covariate effects are also discussed.
The discussion gives a clear account of the various pros and cons of direct regression of the cumulative incidence functions. In particular, an obvious, although perhaps not always sufficiently emphasized issue is that if, in a model with two causes, a Fine-Gray (or other direct model) is fitted to the first cause, and another to the second cause, the resulting predictions will not necessarily have the property that an issue that is not problematic if the second cause is essentially a nuisance issue, but obviously problematic if both causes are of interest. In such cases regression of the cause-specific-hazards is preferable even if it makes interpreting the effect on the cumulative intensity functions more difficult.

Semiparametric transformation models for current status data with informative censoring

Chyong-Mei Chen, Tai-Fang Lu, Man-Hua Chen and Chao-Min Hsu have a new paper in Biometrical Journal. In common with the recent paper by Wang et al, this considers the estimation of current status data under informative censoring. Here, rather than using a copula to describe the dependence between censoring and failure time distributions, a shared frailty is assumed between the censoring intensity and the failure intensity. The frailty is assumed to be log-normal such that and Covariate effects are also allowed for via a general class of transformation models. For estimation, the authors approximate the semi-parametric maximum likelihood estimate by assuming that the conditional intensities, for the censoring and failure events, are piecewise constant functions with an arbitrarily chosen set of change points. Since maximization of the likelihood requires estimation of a large number of unknown parameters and integration of the frailty distribution, the authors propose an EM algorithm. The method attempts to non-parametrically estimate the failure and censoring time distributions and also the variance of the frailty term. While the assumed dependence between T & C is reasonably restrictive, ie. the frailty could feasible have appeared as within the intensity for C allowing other types of dependence. Nevertheless, even with the restrictions it is not clear how the overall model is identifiable. We can only observe where 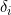is an indicator for whether the failure has occurred by censoring time 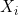. Log-normal frailties are not particularly nice computationally, whereas a Gamma frailty would allow some tractability. In the case of a shared frailty it can be shown that the marginal distribution of censoring times is and the conditional probability of a failure by time X is given by The problem is that we can vary the value of v and find new cumulative intensity functions which will result in the same distribution functions. The addition of covariates via a particular model facilitates some degree of identifiability but, in a similar way to frailty terms in univariate Cox-proportional hazard models, this could just as easily be describing misspecification of the covariate model rather than true dependence.