Fitting and Interpreting Continuous-Time Latent Markov Models for Panel Data

Jane Lange and Vladimir Minin have a paper currently available as a University of Washington Working paper. This considers the computational aspects of fitting a latent continuous time Markov model to multi-state interval censored or panel data. The latent continuous time Markov model proposed is essentially a generalization of the phase-type semi-Markov models considered by Titman and Sharples. It is assumed that for each observable state r, there exist 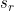latent states: 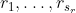Observation in state r can correspond to occupation into any one of these latent states. This induces a type of hidden Markov model and can allow the observed process to be semi-Markov. Lange and Minin propose an EM algorithm to fit the model and compare this with other possible optimization techniques, concluding that their EM algorithm generally performs better, both in terms of reliability and speed of convergence. On this issue, it might have been worth considering the performance of, say, L-BFGS-B (or other constrained optimization methods) using the natural [0,Inf) range for the transition intensities, because many convergence problems for BFGS are due to cases where the true value is near (or at) zero and the exponential parameterization means it never gets there. **Update: This paper is now published in Statistics in Medicine.