A multistate modelling approach for pancreatic cancer development in genetically high risk families

Kolamunnage-Dona, Vitone, Greenhalf, Henderson and Williamson have a new paper in Applied Statistics. This uses a competing risks model with shared frailties to model data on the progression of pancreatic cancer in the presence of clustering and informative censoring. Clustering is present due to data being available on patients from the same family groups. A patient having a resection causes censoring of the main event, time to pancreatic cancer, but is likely to be informative. This is dealt with by allowing the cause-specific hazards to depend on the same frailty term. The methodology in the paper is very similar to that of Huang and Wolfe (Biometrics, 2002), the only extension being that the current formulation allows for the possibility of time dependent covariates. It isn't clear what if any complication this adds to the original procedure in Huang and Wolfe. An MCEM algorithm is used where the E-step is approximated by using Metropolis-Hastings in order to calculate the required expected quantities. It's not clear what the authors mean when they say the Metropolis-Hastings step use "a vague prior for the frailty variance." Hopefully they mean an improper uniform prior as otherwise they would be pointlessly adding Bayesian features to an otherwise frequentist estimating procedure. On a related computational point, since the random effect for each cluster is one dimensional, I suspect using a Laplace approximation to compute the required integrals at each step would perform quite well and be a lot faster than using Metropolis-Hastings

In the analysis there does seem evidence for a shared frailty within clusters, but it appears that the parameter which links the frailty in the time to pancreatic cancer to the time to resection intensity is hard to identify having a very wide 95% confidence interval encompassing strong negative dependence through independence to strong positive dependence. The typical cluster size in the data is quite small (e.g. median is 3) and this is probably insufficient as you would ideally need some subjects to fail and some to be informatively censored in each cluster to assess their association. The point estimate is negative implying a counter intuitive negative association between resection and pancreatic cancer. The authors suggest as a model extension to allow a specific bivariate frailty linking competing risks (presumably within individuals?) - which is unlikely to be helpful.

Mixture distributions in multi-state modelling: Some considerations in a study of psoriatic arthritis

Aidan O'Keeffe, Brian Tom and Vern Farewell have a new paper in Statistics in Medicine. This considers random effects models for clustered multi-state models, specifically considering the psoriatic arthritis example considered in their previous paper. The particular emphasis in the current paper is comparing models using a continuous gamma frailty term with an extended model that additionally allows a "stayer" component. The latter can be thought of as a joining of the continuous random effects model (e.g. Cook et al 2004) and the "mover-stayer" model (e.g. Cook et al 2002). In a discussion on random effects, particularly where there is a question of finite mass points, it is strange there is no mention of the non-parametric mixing distribution (Laird, JASA 1978). While this hasn't really been considered for continuous time processes (the nearest example is Frydman's model) it wouldn't be particularly hard to implement at least the (not entirely reliable) EM algorithm type approach used in discrete-time by Maruotti and Rocci. The apparent presence or absence of a "stayer" component is likely to be heavily dependent on the parametric assumptions made about the rest of the mixing distribution. A very small random effect is indistinguishable from a zero random effect. The authors do emphasize the need to consider several possible mover-stayer models and consider the biological plausibility of them. It is also worth mentioning that all these issues will also hinge on the appropriateness of other assumes e.g. conditionally time homogeneous Markov processes.

Efficient computation of nonparametric survival functions via a hierarchical mixture formulation

Yong Wang and Stephen Taylor have a new paper in Statistics and Computing. This develops a new algorithm for computing the non-parametric maximum likelihood estimate for interval-censored (or part interval-censored) survival data. The problem has a mixture representation (first noted by Bohning et al, Biometrika 1996) and hence methods for finding the NPMLE of a mixing distribution can be applied (for instance the Constrained Newton method of Wang (2007, JRSS B). However, each iteration of the constrained Newton method requires the solution of a constrained least squares problem. If the overall sample size is large, and/or the data are composed of a proportion of exact as well as interval censored observations, the set of candidate support intervals for the NPMLE will be large and the constrained LS problem may be computationally expensive. Wang and Taylor propose to re-formulate the problem as a hierarchy of blocks of intervals. The new algorithm is shown to work well regardless of the sample size of the data and proportion of exactly observed failure times (indeed it essentially tends to the standard constrained Newton algorithm for small samples). However, it is most useful for very large sample sizes and where the proportion of exact observations (and hence unique candidate support points) is high. One thing that looks slightly unfair about the comparison of algorithms was the use of the Icens package to implement some of the older algorithms. While algorithms like EM are obviously inferior, the fact that they are implemented entirely in R whereas others like the support reduction algorithm in MLEcens are implemented in C, make comparison of computation times difficult. However, it is obviously beyond expectations for an author to have to program all algorithms in an equally efficient way!

Bayesian analysis of a disability model for lung cancer survival

Armero, Cabras, Castellanos, Perra, Quirós, Oruezábal and Sánchez-Rubio have a new paper in Statistical Methods in Medical Research. This develops a Bayesian three-state illness-death type model to the progression and survival of lung cancer patients. The data considered are assumed to be complete up to right censoring (in reality there may be some interval censoring but the authors argue the patients can be considered `quasi-continuously' followed. A Weibull semi-Markov model is assumed for the transition intensities and covariates are accommodated via an accelerated failure time model (it's worth noting that for a Weibull distribution the proportional hazard and accelerated failure time models are equivalent up to reparameterization). A feature of the dataset used is the rather small sample size (35 patients) which is perhaps the strongest reason for taking a parametric and Bayesian approach in this case.

Fitting and Interpreting Continuous-Time Latent Markov Models for Panel Data

Jane Lange and Vladimir Minin have a paper currently available as a University of Washington Working paper. This considers the computational aspects of fitting a latent continuous time Markov model to multi-state interval censored or panel data. The latent continuous time Markov model proposed is essentially a generalization of the phase-type semi-Markov models considered by Titman and Sharples. It is assumed that for each observable state r, there exist 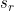latent states: 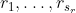Observation in state r can correspond to occupation into any one of these latent states. This induces a type of hidden Markov model and can allow the observed process to be semi-Markov. Lange and Minin propose an EM algorithm to fit the model and compare this with other possible optimization techniques, concluding that their EM algorithm generally performs better, both in terms of reliability and speed of convergence. On this issue, it might have been worth considering the performance of, say, L-BFGS-B (or other constrained optimization methods) using the natural [0,Inf) range for the transition intensities, because many convergence problems for BFGS are due to cases where the true value is near (or at) zero and the exponential parameterization means it never gets there. **Update: This paper is now published in Statistics in Medicine.

Nonparametric estimation of current status data with dependent censoring

Chunjie Wang, Jianguo Sun, Liuquan Sun, Jie Zhou and Dehui Wang have a new paper in Lifetime Data Analysis. This considers estimation of the survivor distribution for current status data when there is dependence between the observation and survival times. Standard current status data models assume that the observation time X is independent of the survival time T. The authors note that from current status data it is possible to estimate the distribution of the observation times and (or with an analogous quantity: ) and that these quantities uniquely define the marginal distribution of T, the (somewhat large) caveat being that the copula linking F and G must be fully specified. To estimate F(x) from observed data, they suggest considering the identity: where and replacing the left hand side and G(x) with empirical quantities to obtain where , which is then solved for F(x). This approach to estimation seems a little bit clunky particularly because the resultant F(x) are not guaranteed to be monotonically increasing in x and do not seem to be guaranteed to be in [0,1] either. While they suggest a modification to let to coerce the estimate to be monotonic, it seems that a more efficient estimator would use some variant of the pool-adjacent-violators algorithm at some juncture. The need to fully specify the copula is similar to the situation with misclassified current status data where it is necessary to know the error probabilities. As a sensitivity analysis it has some similarities to the approach for assessing dependent censoring in right-censored parametric survival models by Siannis et al. In the discussion the authors mention the possibility of extension to more general interval censored data. Once there are repeated observations from an individual there may be greater scope to estimate the degree of dependency between observations and the failure time, although an increased amount of modelling of the observation process would probably be required.