Niels Keiding, Oluf Hojbjerg Hansen, Ditte Norbo Sorensen and Remy Slama have a
paper in Scandinavian Journal of Statistics (a
previous version of which was a Department of Biostatistics, Copenhagen, Research Report). The paper gives an overview of methods for estimating the time to pregnancy in couples attempting to have children based on a 'current duration' design. This involves asking couples whether they are currently trying for a baby and if so, how long have they been trying. The resulting sample will be highly length-biased, i.e. we are more likely to sample people who have been trying for a long time. If the incidence rate of new couples trying to become pregnant in the population is constant, then the density of observed durations amongst those couples trying for a child will be:
 = \frac{S(t)}{\int_0^{\infty} S(u) du})
here S(t) needs to be defined as time to pregnancy OR cessation of attempt at pregnancy - no distinction can be made between the two competing events. Similarly the above assumes the expectation of the event time is finite implying
 \rightarrow 0)
as
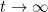
.
S(t) can then be estimated from a direct estimate of g(t) using
 = \hat{g}(t)/\hat{g}(0))
.
Note that, in order for the estimate to make sense, g(t) must be a decreasing function in t.
For parametric inference, Pareto and generalized Gamma distributions are considered. Moreover, the accelerated failure time model is convenient for covariates because of a simple relationship between S & g.
A problem with these methods is the substantial sensitivity of the estimate of S(t) on g(0). This is a particular issue for non-parametric estimation of S, which is based on obtaining a Grenander estimator of g (decreasing non-parametric estimate). This has a tendency to vastly over estimate g(0). A penalized likelihood based on
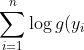 - n \alpha g(0))
where
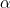
controls the level of penalization, can be used to remedy this problem, as proposed by Woodroofe and Sun (1993, Statistica Sinica). Keiding et al (2002, Biostatistics) gives a good plug-in choice for
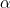
.
On a practical level, calculating this NP maximum penalized likelihood requires computation of the Grenander estimator on a perturbed version of the data. In R, the function grenander in the contributed package fdrtool can compute this. However, it gives an estimate that takes the support of the distribution from the first observation time rather than 0. This can be "bodged" by adding x=0 and y=0 to the ECDF input, e.g. if t is the vector of times:
m <- ecdf(t)
environment(m)$x <- c(0,environment(m)$x)
environment(m)$y <- c(0,environment(m)$y)
class(m) <- "ecdf"
grenander(m)
appears to give the correct estimate.
An alternative to penalization, alluded to by Aalen in his
discussion of the paper, is to only attempt to estimate a conditional survivor distribution, conditional on survival past some small time period. This avoids the dependence on the estimate of g(0) as the estimate of the conditional survivor function is
 = \hat{g}(t)/\hat{g}(t_0))
and
)
is easier to estimate from the available data.
Update: A video presentation by Niels Keiding of this work, from the Applied Statistics conference in Bled, Slovenia is available
here.
No comments:
Post a Comment