Improvement of expectation–maximization algorithm for phase-type distributions with grouped and truncated data

Hiroyuki Okamura, Tadashi Dohi and Kishor S. Trivedi have a new paper in Applied Stochastic Models in Business and Industry. This builds on work by Olsson (Scandinavian Journal of Statistics, 1996) on fitting phase-type distributions to grouped data via an EM algorithm. The authors also have a very similar paper in Performance Evaluation that improves the EM algorithm for completely observed phase-type distributed times using the same methods. The authors of the current paper note that the E-step in Olsson's algorithm requires computation of a convolution of matrix exponentials. This will be computationally intensive, particularly if the order of the phase-type distribution is large. The proposed improvement is to apply a uniformization technique to the computations of these convolutions. For calculation of a matrix exponential, the uniformization technique involves equating the continuous time Markov chain with a discrete time Markov chain and an associated (but independent) Poisson process. This means that

where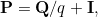 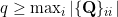and for This approach can also be used to get a formula for the convolution again as a sum weighted over Poisson probabilities. The authors show that using these methods to compute the convolutions of matrix exponentials rather than using the approach of Asmussen et al (which is to formulate the problem in terms of a systems of differential equations that are then solved numerically via a 4th order Runge-Kutta method), gives a fairly substantial improvement in the running time of the algorithm. While the authors improve the EM algorithm, it is debatable whether an EM algorithm approach, which tends to have a convergence rate that depends on the amount of missing data, is optimal for these problems where there is a lot of "missing" data (i.e. the "complete" data involves the total time spent in each latent state of the phase type distribution and the numbers of each type of transition). I suspect quasi-Newton type methods might work better in terms of convergence. However, more generally, given the inherent identifiability problems with these models due to overparametrization, whether the EM or any other algorithm converges to the global optimum is a moot point.