Bo Hu, Liang Li, Xiaofeng Wang and Tom Greene have a new paper in Statistics in Medicine. This develops approaches for summarizing longitudinal and survival data in terms of marginal prevalences. The authors' use of "multistate" is perhaps not entirely in line with its typical usage. They consider data consisting of right censored competing risks data plus additional continuous longitudinal measurements which persist until a competing event has occurred (or censoring). For the purpose of creating a summary measure, the longitudinal measurement can be partitioned into a set of discrete states. There are thus states corresponding to absorbing competing risks plus a series of transient states corresponding to the longitudinal measurements. The aim of the paper is to develop a nonparametric estimate of the marginal probability of being in a particular state at a particular time.
The approach taken is firstly to use standard non-parametric estimates for competing risks data to get estimates of the probability of being in each of the absorbing states. For the longitudinal part, it is assumed that the "true" longitudinal process is not directly observed but instead observed with measurement error. As a consequence the authors propose to use smoothing splines to get an individual estimate of each subject's true trajectory. The combined state occupancy probability at time t for a longitudinal state then consists of the overall survival probability from the competing risks multiplied by the proportion of subjects still at risk at time t who are estimated (on the basis of their spline smooth) to be within that interval. The probability of being in an absorbing state is computed directly from the competing risks estimates. Overall a stacked probability plot consisting of the stacked CIFs for each of the competing risks plus the (not necessarily monotonic) partition of the longitudinal states.
The use of individual smoothing splines seems to present practical problems. Firstly, it assumes that the true longitudinal process is itself in some way "smooth". In some cases the change in state in a biological process may manifest itself in a rapid collapse of a biomarker. Secondly, it seems to require a relatively large number of longitudinal measurements per person in order to get a reasonable estimate of their "true" process. Presumably the level of the longitudinal measure is likely to have a bearing on the cause-specific-hazards of the competing risks. The occurrence of one of the competing risks is thus informative for the longitudinal process. The authors claim to have got around this by averaging only over people currently in the risk set at time t. However, the longitudinal measurements are intermittent. If they are sparse then someone may be observed at say 1 year, 2 years and then die at 10 years. The method would estimate a smooth spline based on years 1 and 2 and extrapolate up to 10 years not using the fact the subject died at 10 years. Similarly, there might be one or fewer longitudinal observations before a competing event for some patients making estimation of the true trajectory near impossible. Also, the estimator as it stands attempts no weighting to take account of the relative uncertainties about different individuals true trajectories at particular times. Overall as a descriptive tool it may be useful in some circumstances; primarily if subjects has regular longitudinal measurements. In this respect it is similar to the "prevalence counts" (Gentleman et al, 1994) method of obtaining non-parametric prevalence estimates for interval censored multi-state data.
In the appendix, a brief description is given of an approach to allowing the transition probabilities between states to be calculated. They only illustrate the method for a case of going from a longitudinal state to an absorbing state (presumably the procedure for transitions between longitudinal states would be different). Nevertheless, there doesn't seem to be any guarantee that estimated transition probabilities will lie in [0,1].
Sunday, 29 April 2012
Nonparametric multistate representations of survival and longitudinal data with measurement error
Thursday, 26 April 2012
Improvement of expectation–maximization algorithm for phase-type distributions with grouped and truncated data
Hiroyuki Okamura, Tadashi Dohi and Kishor S. Trivedi have a new paper in Applied Stochastic Models in Business and Industry. This builds on work by Olsson (Scandinavian Journal of Statistics, 1996) on fitting phase-type distributions to grouped data via an EM algorithm. The authors also have a very similar paper in Performance Evaluation that improves the EM algorithm for completely observed phase-type distributed times using the same methods. The authors of the current paper note that the E-step in Olsson's algorithm requires computation of a convolution of matrix exponentials. This will be computationally intensive, particularly if the order of the phase-type distribution is large. The proposed improvement is to apply a uniformization technique to the computations of these convolutions. For calculation of a matrix exponential, the uniformization technique involves equating the continuous time Markov chain with a discrete time Markov chain and an associated (but independent) Poisson process. This means that
 = \sum_{i=0}^{\infty} p(i,qt)\mathbf{P}^{i})
where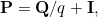
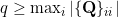 and
and  = P(N = i)) for
for .) This approach can also be used to get a formula for the convolution again as a sum weighted over Poisson probabilities.
The authors show that using these methods to compute the convolutions of matrix exponentials rather than using the approach of Asmussen et al (which is to formulate the problem in terms of a systems of differential equations that are then solved numerically via a 4th order Runge-Kutta method), gives a fairly substantial improvement in the running time of the algorithm.
While the authors improve the EM algorithm, it is debatable whether an EM algorithm approach, which tends to have a convergence rate that depends on the amount of missing data, is optimal for these problems where there is a lot of "missing" data (i.e. the "complete" data involves the total time spent in each latent state of the phase type distribution and the numbers of each type of transition). I suspect quasi-Newton type methods might work better in terms of convergence. However, more generally, given the inherent identifiability problems with these models due to overparametrization, whether the EM or any other algorithm converges to the global optimum is a moot point.
This approach can also be used to get a formula for the convolution again as a sum weighted over Poisson probabilities.
The authors show that using these methods to compute the convolutions of matrix exponentials rather than using the approach of Asmussen et al (which is to formulate the problem in terms of a systems of differential equations that are then solved numerically via a 4th order Runge-Kutta method), gives a fairly substantial improvement in the running time of the algorithm.
While the authors improve the EM algorithm, it is debatable whether an EM algorithm approach, which tends to have a convergence rate that depends on the amount of missing data, is optimal for these problems where there is a lot of "missing" data (i.e. the "complete" data involves the total time spent in each latent state of the phase type distribution and the numbers of each type of transition). I suspect quasi-Newton type methods might work better in terms of convergence. However, more generally, given the inherent identifiability problems with these models due to overparametrization, whether the EM or any other algorithm converges to the global optimum is a moot point.
where
Wednesday, 25 April 2012
Use of alternative time scales in Cox proportional hazard models: implications for time-varying environmental exposures
Beth Griffin, Garnet Anderson, Regina Shih and Eric Whitsel have a new paper in Statistics in Medicine. The paper investigates the use of different time scales (e.g. other than either study time or patient age) in cohort studies analysed via Cox proportional hazard models. Of particular focus is the use of calendar time as an alternative time scale, with a motivation in the variation of environmental exposures over time. They perform a simulation study considering two scenarios for the relationship between a time varying environmental exposure variable and calendar year. In the first scenario these are made independent, while the second scenario assumes a linear relationship. As one might expect, when there is no correlation between calendar time and the time dependent environmental exposure, estimates are unbiased regardless of the choice of time scale. When a linear relationship exists then models that account for calendar time, either as the primary time scale or as additional covariates in the model. Again, this isn't necessarily surprising because the model is effectively attempting to include a year effect twice, once in the baseline hazard and again as a large component of the time dependent covariate, e.g. you are fitting a model with "mean environmental exposure in year t" and "environmental exposure" as covariates and expecting the latter to have the correct coefficient. The paper only gives a simulation study, I don't think it would have been that hard to have given some basic theoretical results in addition to the simulations.
The conclusion of the paper, albeit with caveats, is that attempting to adjust for calendar time because you suspect the environmental exposure may be correlated with time is not useful. Clearly if there are other reasons to suspect that calendar year may be important to the hazard in a study then there is an inherent lack of information in the study to establish whether the environmental exposure is directly affecting the hazard or whether it is an indirect effect due to the association with calendar time. Ideally, one would look for other calendar time dependent covariates (e.g. prevailing treatment policy regimes etc.) and perhaps try directly adjusting for them rather than calendar time itself.
The conclusion of the paper, albeit with caveats, is that attempting to adjust for calendar time because you suspect the environmental exposure may be correlated with time is not useful. Clearly if there are other reasons to suspect that calendar year may be important to the hazard in a study then there is an inherent lack of information in the study to establish whether the environmental exposure is directly affecting the hazard or whether it is an indirect effect due to the association with calendar time. Ideally, one would look for other calendar time dependent covariates (e.g. prevailing treatment policy regimes etc.) and perhaps try directly adjusting for them rather than calendar time itself.
Wednesday, 18 April 2012
Bayesian inference of the fully specified subdistribution model for survival data with competing risks
Miaomiao Ge and Ming-Hui Chen have a new paper in Lifetime Data Analysis. This considers methods for Bayesian inference in the Fine-Gray model for competing risks. In order to perform the Bayesian analysis it is necessary to fully specify the model for the competing risk(s) that are not of direct interest in the analysis. Ge and Chen propose a model in which for failure time 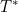 ,
,
 = P(T^{*} \leq t, \delta = 2) = M_2(t)P(\delta = 2)) and a proportional hazards model affects
and a proportional hazards model affects ) via
via
 = 1 - \exp{\{-H_{20}(t)\exp{(\mathbf{x}^{T}\beta_2)}\}}) .
.
Note that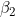 does not affect
does not affect ) or
or ) .
.
The authors consider approaches to non-parametric Bayesian inference using Gamma process priors, but also use piecewise constant hazard models (with fixed cut points) where the hazard in each time period has an independent gamma prior.
Note that
The authors consider approaches to non-parametric Bayesian inference using Gamma process priors, but also use piecewise constant hazard models (with fixed cut points) where the hazard in each time period has an independent gamma prior.
Subscribe to:
Comments (Atom)