A Measure of Explained Variation for Event History Data

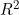
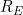
Stare, Perme and Henderson have a new paper in Biometrics. This develops a measure of explained variation, in some sense analogous to for linear regression, for survival and event history data. The measure, denoted is based on considering all individuals at risk at event times and considering the rank of the individual that had the event, in terms of the estimated intensities under a null model (e.g. assuming homogeneity of intensities across subjects), the current model (e.g. a Cox regression or Aalen additive hazards model) and a perfect model (where the individual who had an event always has the greatest intensity). 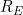In the case of complete observation, is the ratio of the sum of the difference in ranks between the null and current model and the sum of the difference in ranks between the null and the perfect model. 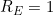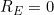Thus would represent perfect prediction whilst would imply a model as good as the null model. 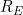Note that it is possible to have < 0 when the predictions are worse than under a null model.

When there is not complete observation a weighted version is proposed. Weighting is based on the inverse probability of being under observation. For data subject to right-censoring independent of covariates, this can be estimated using a 'backwards' Kaplan-Meier estimate of the censoring distribution. The weighting occurs in two places. Firstly, the contribution of each event time is weighted to account for missing event times. Secondly, at each event time the contribution to the ranking of each individual is weighted by the probability of observation. This latter weighting is relevant when censoring is dependent on covariates.

A very nice property of the measure is that a local version relevant to a subset of the observation period is possible. This is a useful alternative way of diagnosing, for instance, time dependent covariate effects, e.g. lack of fit will manifest itself in a deterioration in .

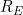
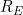
One practical drawback of the measure is the requirement to model the "under observation" probability. For instance, left-truncated data would require some joint model of left-truncation and right-censoring times. In the context of Cox-Markov multi-state models, it would in principle be possible to compute a separate for the models for each intensity. However, there will be inherent left-truncation and its not clear whether weighting to get the data under complete observation makes sense in this case because complete observation is unattainable in reality since subjects can only occupy one state at any given time.

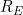
The authors provide R code to calculate for models fitted in the survival package. However, left truncated data is not currently accommodated.