Computation of the asymptotic null distribution of goodness-of-fit tests for multi-state models

Andrew Titman has a new paper in Lifetime Data Analysis. This is essentially a continuation of previous papers by Aguirre-Hernandez and Farewell and by Titman and Sharples on Pearson-type goodness-of-fit tests for Markov and hidden Markov models on panel observed data. A practical problem with the tests is that the null distribution depends on the true parameter value and the observation scheme and that a chi-squared approximation can perform inadequately. A parametric bootstrap could be used to find the upper 95% point of the distribution. However, for many models the re-fitting required may take an unacceptable amount of time. Titman shows that, conditional on a fixed observation scheme, the asymptotic distribution can be expressed as a weighted sum of independent 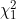random variables, where the weights depend on the true parameter values. A simulation study shows that computing the weights based on the maximum likelihood estimate of the parameter values, gives tests of close to the appropriate size for realistic sample sizes. The method can be applied to both Markov and misclassification-type hidden Markov models, but only when all transitions are interval-censored.