Statistical Analysis of Illness-Death Processes and Semicompeting Risks Data

Xu, Kalbfleisch and Tai have a new paper in Biometrics. They make a compelling case against a latent failure times approach to the analysis of semi-competing risks data, advocating to instead take a classical cause-specific hazards approach. Moreover, they note that semi-competing risks is essentially just an illness-death model. They consider models where the intensities have a shared Gamma frailty and present methods for (Non-parametric) maximum likelihood estimation. In addition, covariates can be included acting proportionally on the conditional hazards (an alternative approach with proportionality on the marginal hazards is also outlined).

Semi-Markov models with phase-type sojourn distributions

Titman and Sharples have a new paper in Biometrics. This concerns the fitting of semi-Markov models to panel observed data. They propose to fit models where the sojourn time in each state has a phase-type sojourn distribution - i.e. corresponds to the time to absorption of some time homogeneous Markov model. The advantage of this specification is that, unlike general semi-Markov models, the likelihood remains analytically tractable, falling within a hidden Markov model framework. This also makes the extension to models where the observations are subject to misclassification error straightforward, at least theoretically. A two-phase Coxian phase-type distribution is proposed for the sojourn time, allowing increasing, decreasing or constant hazards with respect to time since entry into the state.

While the phase-type framework makes computation of the likelihood more straightforward, model fitting is still potentially problematic due to possible problems of parameter estimability. Also since certain parameters of the phase-type model are unidentifiable under a Markov model meaning an (approximate) modified likelihood ratio test is required to test the Markov assumption.

Mstate: Data preparation, estimation and prediction in multi-state models. R package.

A significant barrier to the widespread use of multi-state models in applied statistics has been the lack of software. For right-censored data, models on the transition intensities can be fitted straightforwardly using standard survival modelling techniques (e.g. Cox regression and Nelson-Aalen estimators). However, for estimates of cumulative incidence functions, state occupation probabilities and moreover their standard errors, with a few exceptions it was generally necessary to make your own code. Hein Putter, Marta Fiocco and Liesbeth de Wreede have created the R package mstate, this provides a general framework for fitting right-censored and left-truncated non-parametric and semi-parametric multi-state models. The package exploits the existing R package survival to fit the models to intensities but also provides routines to calculate transition probabilities and their standard errors of the overall multi-state model. This is clearly a very useful tool. One small drawback of the package is that the routines such as those to calculate the transition probabilities appear to be coded entirely in R. As a result computation is the not as fast as might be hoped. The package etm by Arthur Allignol, which only computes the Aalen-Johansen estimator, may be preferable in terms of speed when only a non-parametric model is required as this incorporates some C code.

Update: An article on mstate in Computer Methods and Programs in Biomedicine is now available.

Further Update: A further paper on mstate is now available in the Journal of Statistical Software.

Computation of the asymptotic null distribution of goodness-of-fit tests for multi-state models

Andrew Titman has a new paper in Lifetime Data Analysis. This is essentially a continuation of previous papers by Aguirre-Hernandez and Farewell and by Titman and Sharples on Pearson-type goodness-of-fit tests for Markov and hidden Markov models on panel observed data. A practical problem with the tests is that the null distribution depends on the true parameter value and the observation scheme and that a chi-squared approximation can perform inadequately. A parametric bootstrap could be used to find the upper 95% point of the distribution. However, for many models the re-fitting required may take an unacceptable amount of time. Titman shows that, conditional on a fixed observation scheme, the asymptotic distribution can be expressed as a weighted sum of independent 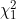random variables, where the weights depend on the true parameter values. A simulation study shows that computing the weights based on the maximum likelihood estimate of the parameter values, gives tests of close to the appropriate size for realistic sample sizes. The method can be applied to both Markov and misclassification-type hidden Markov models, but only when all transitions are interval-censored.

Analyzing longitudinal data with patients in different disease states during follow-up and death as final state

Le Cessie, de Vries, Buijs and Post have a new paper in Statistics in Medicine. This is concerned with estimating mean quality of life in breast cancer patients at different time points. Standard approaches to analyzing such longitudinal data would be generalized estimating equations (GEE). However, observations are often missing and assuming such data are missing completely at random (MCAR) is unrealistic or even missing at random. In the current study a three-state progressive illness-death model is considered where the illness state refers to presence of a relapse. Both Markov (or clock-forward) and semi-Markov (or clock-reset) models are considered. There was continuous observation of the illness-death process, whereas the quality of life was observed at a common set of time points. The authors propose to model quality of life scores conditional on the state occupied in the multi-state model. A more realistic missingness model can then be adopted by assuming MAR conditional on the occupied state. Inverse probability weighting is used to deal with the missing data. Standard error estimation is performed by bootstrapping.

While the model gives an improved picture compared to ignoring the disease state, the model still makes the assumption that quality of life is dependent on time and current disease state but not on the time since entry into the current disease state.