Donglin Zeng, Qingxia Chen, Ming-Hui Chen and Joseph Ibrahim have a new paper in Biometrika. This considers the problem of comparing survival times in clinical trials in which there may be an intermediate disease progression event which may cause the treatment (if initially randomized to control) to be switched. Previous approaches to this problem have been proposed, through univariate survival methods. Here, the authors instead consider a multi-state (semi-competing risks) model. Interest lies in determining the survival distribution under a treatment given no switching.
In line with the other recent Biometrika paper, a pattern-mixture type parametrization is adopted in that a logistic regression component is defined for the probability of progression before death and separate conditional hazard function for time to death given no-progression and time to progression given progression, plus time to death from progression. Switching is assumed to be non-informative of outcome given that progression has occurred and the act of switching has a proportional effect on the hazard of death from progression.
Besides rigorous proofs of results, there doesn't seem to be any substantial conceptual advances in the paper, though it does seem to represent a better approach to the specific problem than the previous approaches.
Thursday, 5 January 2012
Sunday, 1 January 2012
Bayesian analysis of multistate event history data: beta-Dirichlet process prior
Yongdai Kim, Lancelot James and Rafael Weissbach have a new paper in Biometrika. This develops a conjugate prior process suitable for non-parametric and semi-parametric Bayesian modelling of right-censored multi-state Markov data. The model is parametrised in terms of the sum of the intensities out of each state
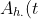 = \sum_{j \neq h} A_{hj}(t) "A_{h.}(t) = \sum_{j \neq h} A_{hj}(t)")
and instantaneous transition probabilities
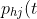 = dA_{hj}(t)/dA_{h.}(t) "p_{hj}(t) = dA_{hj}(t)/dA_{h.}(t)")
A possible choice for a prior process is a Dirichlet distribution but this is not independent in the limit of a continuous time process. Instead the authors propose a new beta-Dirichlet process consisting of a beta distributed part which determines the increment in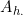
(between 0 and 1) and a Dirichlet part determining the instantaneous transition probabilities for each particular transition. The authors prove this prior process is conjugate in the continuous limit.
A semi-parametric regression model is proposed, which the authors term as a semi-proportional intensities model. This consists of a proportional intensities model for the all-cause hazard of exiting state h and a multinomial type model for the instantaneous transition probabilities out of state h and bears some resemblance to the vertical modeling parametrization for competing risks regression.
In an aside the authors claim that interval censoring can easily be dealt with by treating the unknown transition time as missing data that can be accounted for in the Gibbs sampling. This only works under the assumption that only one transition can have occurred between examination times. While other authors have made this assumption (e.g. Foucher et al 2007) it is dubious to say the least and likely to result in biased estimates. Similarly, the authors claim right-censoring can be dealt with by treating a censoring event as an additional state. While this will obviously allow the observed process to be modelled, it is not clear how this approach would allow the underlying process (without censoring) is estimated?
and instantaneous transition probabilities
A possible choice for a prior process is a Dirichlet distribution but this is not independent in the limit of a continuous time process. Instead the authors propose a new beta-Dirichlet process consisting of a beta distributed part which determines the increment in
A semi-parametric regression model is proposed, which the authors term as a semi-proportional intensities model. This consists of a proportional intensities model for the all-cause hazard of exiting state h and a multinomial type model for the instantaneous transition probabilities out of state h and bears some resemblance to the vertical modeling parametrization for competing risks regression.
In an aside the authors claim that interval censoring can easily be dealt with by treating the unknown transition time as missing data that can be accounted for in the Gibbs sampling. This only works under the assumption that only one transition can have occurred between examination times. While other authors have made this assumption (e.g. Foucher et al 2007) it is dubious to say the least and likely to result in biased estimates. Similarly, the authors claim right-censoring can be dealt with by treating a censoring event as an additional state. While this will obviously allow the observed process to be modelled, it is not clear how this approach would allow the underlying process (without censoring) is estimated?
Subscribe to:
Posts (Atom)