Optimal designs for epidemiologic longitudinal studies with binary outcomes

Juha Mehtala ,Kari Auranen and Sangita Kulathina have a new paper in Statistical Methods in Medical Research. This considers optimal design of panel studies for binary stochastic processes which are assumed to be time-homogeneous Markov. Optimality is assessed based on the trace of the expected Fisher information. The authors also consider a two-phase design where the time spacing is improved upon after the first stage.

This paper, and also the paper by Hwang and Brookmeyer, restrict attention to equally spaced designs. Potentially, there may be efficiency gains from having unequally spaced observations particularly if equilibrium is not assumed at time 0. Moreover, an adaptive "doctor's care" type design where the gap to the next clinic visit depends on the current state is also likely to give some efficiency gains. There has been relatively little work on design for multi-state models. Clearly the efficiency gains achieved in practice depend on the accuracy of the initial assumptions about the true parameter values, although if a two-phase approach is possible it can militate against this. In complicated studies a simple relationship between expected parameter values and optimal design may not exist but may nevertheless be calculable by bespoke numerical optimization. Perhaps the main problem is that studies are rarely designed with an eventual multi-state model analysis in mind.

A dynamic model for the risk of bladder cancer progression

Núria Porta, M. Luz Calle, Núria Malats and Guadalupe Gómez have a new paper in Statistics in Medicine. This develops a model for progression of bladder cancer with particular emphasis on predicting future risk given events up to a certain point in time.

In many ways the paper is taking a similar approach to Cortese and Andersen in explicitly modelling a time dependent covariate (here recurrence) in order to obtain predictions.
They fit a semi-parametric Cox Markov multi-state model to the data and define a prediction process


where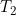 is the time of the second event, 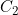is the type of the second event where P denotes progression and represents the history of the process up to time t. Analogously to outcome measures like the cumulative incidence functions, this predictive process is a function of the transition intensities. They also consider time dependent ROC curves to assess the improvement in classification accuracy that can be achieved by taking into account past history in addition to baseline characteristics.

Estimating net transition probabilities from cross-sectional data with application to risk factors in chronic disease modeling

van de Kassteele, Hoogenveen, Engelfriet, van Baal and Boshuizen have a new paper in Statistics in Medicine. This considers the estimation of the transition probabilities in a non-homogeneous discrete-time Markov model, when the only available information is cross-sectional data, i.e. for each time (or age) we have only a sample of individuals and their state occupancy from which the prevalence at that time can be estimated. Note this type of observation is more extreme than aggregate data, considered for instance by Crowder and Stephens, where we only have prevalences at a series of times but the state occupation counts correspond to the same set of subjects.

The authors take a novel, if slightly quirky approach, to estimation. They firstly use P-splines to smooth the observed prevalences. Having obtained these they then need to translate them into transition probabilities. This is not straightforward since there are more parameters to estimate than degrees of freedom. To get around this problem the authors restrict their estimate to be the values that minimize a transportation problem. Essentially this assigns a "cost" to transitions, penalizing those to further apart states and giving zero cost to remaining in the same state. So gives a solution that aims to maximize the diagonals of the transition probability matrices whilst constraining the prevalences to take their P-spline smoothed values.

What is absent from the paper is formal justification for the approach. Presumably a similar outcome could be achieved by applying a penalized likelihood approach, possibly formulating the problem in continuous time and setting the penalty to be the magnitude of the transition intensities (and possibly their derivatives). However, this would require some calibration to choose the penalty weights and it is not clear how this would be done (the usual approach of cross-validation would not work here).

Intermittent observation of time-dependent explanatory variables: a multistate modelling approach

Brian Tom and Vern Farewell have a new paper in Statistics in Medicine. This considers the problem of estimating the effect of a time dependent covariate on a multi-state process when both the disease process of interest and the time dependent covariate are only intermittently observed. The most common existing approach to dealing with this problem is to assume that the time dependent covariate is constant between observations, taking the last observed value. The authors instead jointly model the two processes as an expanded multi-state model, if the disease process had n states and the covariate process m states the resulting process will have 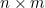states. An additional assumption, that movements in the covariate process are not directly affected by the state of the disease process, is also made.

A simulation study is performed which shows that the approach of assuming the time dependent covariate is constant leads to biased estimates, particularly when there is a bias in the trend of the covariate process (e.g. much more likely to decrease than increase in value).

The overall approach taken by the authors is to model their way out of difficulty. They assume that both the disease process of interest and the covariate process are jointly time homogeneous Markov and the validity of the results will depend on these assumptions being correct. As noted by the authors, if the covariate can take more than a small number of values the approach becomes unattractive because of the large number of nuisance parameters required. A point not really emphasized, but related to the analogous approach taken by Cortese and Andersen for continuously observed competing risks data (bizarrely not referenced in this paper despite massive relevance!), is that having modelled the time dependent covariate, the model can then be used to make overall predictions.

One could argue that the convention of following forward the covariate value observed from the previous period is a way of allowing a prediction to be made about the trajectory in the next period. A fairer comparison in some cases might therefore be to look at the bias in estimating the transition probabilities to time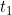 given a covariate variate value of 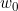at time 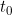. While we would expect these estimates still to be biased, the amount of bias is likely to be less than found by looking at the regression coefficients directly.

An open problem seems to be the development of methods that do not require strong assumptions, or else are robust to misspecification, to deal with intermittently observed time dependent covariates.