Parametric inference for time-to-failure in multi-state semi-Markov models: A comparison of marginal and process approaches

Yang Yang and Vijayan Nair have a new paper in Canadian Journal of Statistics as part of the Kalbfleisch and Lawless special issue. The paper considers inference for progressive semi-Markov processes for complete, right-censored and interval-censored data for parametric models with Gamma or inverse Gamma sojourn distributions. The advantage of considering Gamma or inverse Gamma distributions is that their convolutions have a closed form meaning the overall failure (absorption) time distribution is available in closed form. Inference using only the time-to-failure data is therefore relatively straightforward. The main focus of the paper is investigating the loss in efficiency of only using time-to-failure data when additional data on intermediate states (either through continuous observation or panel data) are available. The authors show that the loss in efficiency can be rather substantial, particularly if interest lies in making predictions about time to failure given an existing process history rather than just mean or median survival. It is therefore suggested that information on intermediate states should be incorporated where possible despite this presenting computationally difficulties in the case of panel data.

Combined survival analysis of cardiac patients by a Cox PH model and a Markov chain

Michal Shauly, Gad Rabinowitz, Harel Gilutz and Yisrael Parmet have a new paper in Lifetime Data Analysis. This considers methods for modelling the effect of a mixture of time dependent and time constant covariates on overall survival, with the complication that the time dependent covariates are only observed at a discrete set of time points. They propose to firstly fit a Cox proportional hazard model assuming all covariates are fixed at their baseline values. The main modelling approach is to assume a discrete-time homogeneous Markov model with states corresponding to the combinations of the time dependent covariates (which are categorical or need to be categorized) and death. Transitions between all covariates states are assumed to be possible between each time point. The Cox model is used to determine which of the constant covariates should be considered in the Markov model. For this the authors propose to again categorize the covariates and consider a separate Markov model for each level of the covariates. Having obtained the estimates from the Markov models, it is then possible to calculate expected survival times for patients conditional on their baseline characteristics.

In general the approach proposed is reasonably sensible. However, there is panel data available for the time dependent covariates. It therefore seems possible to fit a time continuous Markov model to the data using methods appropriate for panel data (e.g. Kalbfleisch and Lawless, 1985). This approach has the advantage that the exact time of the death events can still be used.

The authors rely on categorization throughout. While this seems necessary for the time dependent covariates, there seems scope for using multinomial logit models for other covariates. Similarly, by allowing a different mortality probability for each combination of covariates they are effectively fitting covariate models with interactions (i.e. the effect of being in covariate level 2 compared to 1, is different depending on which level(s) of the other time dependent covariate(s) a subject is in). While such interactions may be necessary, it might be better to allow simpler models where only the evolution of the time dependent covariates is kept general. This is another advantage of a continuous time model since covariate effects could remain on the hazard (transition intensity) scale as in the Cox PH model.

Finally, the authors give a partial justification of the use of a time homogeneous Markov model through the Cox PH model having an approximately constant baseline hazard. It should be noted that a time homogeneous Markov model does not imply a constant absorption hazard (unless the model begins in the quasi-stationary distribution). Conversely, while a constant hazard might suggest homogeneity more than non-homogeneity, it is nevertheless possible to construct non-homogeneous processes with constant (or near constant) marginal absorption hazards. The authors do however report a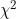 statistic which gives a better justification of homogeneity.