Dantan, Joly, Dartigues and Jacqmin-Gadda have a new paper in Biostatistics. There is a wide literature on joint models of survival with longitudinal data with some extensions for joint competing-risks survival and longitudinal data (e.g. Elashoff et al). Dantan et al develop a joint model for multi-state survival data and longitudinal data. The standard approach to these joint models is to have a random effect that it shared across the model for the survival data (e.g. appearing as a frailty) and the longitudinal model (e.g. random slopes and intercepts in a generalized linear mixed model). Rather than follow this convention, Dantan et al allow a slightly more direct correspondence between the survival and longitudinal parts. Specifically, they have a progressive 4-state multi-state model relating to healthy, pre-diagnosis, illness and death states. The pre-diagnosis state is unobservable and entry into this state corresponds to the time a which the slope of decline in the longitudinal biomarker changes. The model is an extension on the random change-point model proposed by Jacqmin-Gadda et al (Biometrics, 2006), as here it is not necessary to make unrealistic assumptions about death being non-informative censoring for illness.
For the PAQUID dataset on cognitive decline, the baseline transition intensities are of Weibull form for healthy to pre-diagnosis and pre-diagnosis to illness (the latter being Weibull w.r.t time since pre-diagnosis). The hazard of death is assumed to depend only on age (via piecewise constant intensities) and the value of the longitudinal marker, Y(t), but not explicitly on the current disease state. This assumption seems to be primarily for computational reasons.
A limitation of the approach taken in the paper is that dementia is only diagnosed at clinic visits, so in effect is interval censored between the current and last clinic visit. The authors just assume entry into the dementia state occurred at the midpoint between clinic visits. Through simulation in the supplementary materials the authors show this doesn't cause serious bias.
However, a further issue is that the dependency of the dementia age on the observed value of the marker at a clinic visit would presumably mean the assumption of independence between dementia age and observation errors conditional on the random effects (slopes, intercepts and change-time) would be inappropriate. To what extent is the apparent increase in the decline of cognition before diagnosis due to such an artifact?
Monday, 21 March 2011
Wednesday, 16 March 2011
Presmoothing the transition probabilities in the illness-death model
Ana Paula Amorim, Jacobo de Una-Alvarez and Luis Meira-Machado have a new paper in Statistics & Probability Letters. This proposes an estimator for the transition probabilities in a three-state illness-death model under general (i.e. non-Markov conditions). A variant of the estimator by Meira-Machado et al (2006, Lifetime Data Analysis) is proposed, the difference here being the presence of "pre-smoothing". This involves replacing the censoring weights in the estimating equations with parametric estimates of the weights, for instance via a logistic model. They demonstrate that the method results in more efficient estimators of the transition probabilities and appear to be robust to some level of misspecification of the parametric model for the weights.
Wednesday, 9 March 2011
msSurv: Nonparametric Estimation for Multistate Models
Nicole Ferguson, Guy Brock and Somnath Datta have written an R package for non-parametric estimation in multi-state models. To some extent the package covers similar ground to mstate and etm, the focus being on data continuously observed up to right censoring. Unlike mstate there is no possibility of semi-parametric modelling. The main area of new functionality in msSurv is the ability to estimate state entry and exit time distributions, and the ability to cope with state dependent censoring mechanisms using the methodology of Datta and Satten (Biometrics, 2002). As with mstate, all computations appear to be performed within R itself. Thus if a standard Aalen-Johansen type estimate is required, etm is still the best package to use. For instance, the example simulated right censored data provided in the package takes over 3 minutes to fit using msSurv, compared to just 1.2 seconds in etm. Since, for the more bespoke parts of the package, e.g. robust estimates of state occupancy for non-Markov models or state dependent censoring, bootstrapping is required for confidence intervals, the lack of speed of msSurv is a little disappointing.
Update: A paper on the msSurv package has now been published in the Journal of Statistical Software.
Tuesday, 1 March 2011
Modelling time to event with observations made at arbitrary times
Matthew Sperrin and Iain Buchan have a new paper available at the arXiv. This concerns the interesting problem of developing survival models in the presence of time dependent covariates that are only observed at baseline, for data with delayed entry (i.e. left truncation).
A large proportion of the paper is devoted to arguing that in studies where the entry time does not involve an intervention and follow-up is over a long period, it is more appropriate to use age as the primary timescale rather than using study time and including age at entry as a covariate. The latter approach can lead to counterintuitive results where a 50 year old is more likely to survive to 70 than a 55 year old with the same covariate values except age.
The paper is less convincing when it comes to possible solutions to the problem of time dependent covariates only observed at baseline. Their approach is essentially to assume that
 = f(t) + \epsilon_i "z_i(t) = f(t) + \epsilon_i")
for some arbitrary function f(t). Hence it is assumed that the time dependent covariates vary deterministically so that a subject who has lower than average blood pressure aged 30, will have increasing blood pressure as they age but stay at the same (age specific) quantile. Obviously a first issue is how realistic this is, especially for modelling internal covariates. Assuming this model is correct, Sperrin and Buchan propose a two-step procedure in which they firstly regress the observed baseline covariate values on t to estimate f(t). They then use the residuals from this procedure to put into standard proportional hazards or accelerated failure time models. A problem that they freely acknowledge is that the observed baseline covariate values will be biased if they are, for instance, both increasing with age and associated with increased hazard. They suggest, but don't implement, some form of iterative procedure to accommodate this.
They seem to have overlooked a trivial way around this problem: For a Cox proportional hazards models when f(t) is assumed linear with unknown slope v (as in their example), if we observe covariate value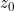
at time 
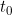then this implies
&=&h_0(t)\exp{\{\beta[z_0 + v(t-t_0)]\}}\\ h(t)&=&\tilde{h}_0(t)\exp{\{\beta[z_0 - vt_0]\}}\\ \end{align*} "\begin{align*} h(t)&=&h_0(t)\exp{\{\beta[z_0 + v(t-t_0)]\}}\\ h(t)&=&\tilde{h}_0(t)\exp{\{\beta[z_0 - vt_0]\}}\\ \end{align*}")
i.e. the deterministic part of the time dependent covariate is merely absorbed into the baseline hazard and it is just necessary to include age at entry as an additional covariate. For non-linear models we have:
 &=& h_0(t)\exp{\{\beta [z_0 + f(t) - f(t_0)]\}}\\ h(t) &=& \tilde{h}_0(t)\exp{\{\beta [z_0 - f(t_0)] \}}\\ \end{align*} "\inline \begin{align*} h(t) &=& h_0(t)\exp{\{\beta [z_0 + f(t) - f(t_0)]\}}\\ h(t) &=& \tilde{h}_0(t)\exp{\{\beta [z_0 - f(t_0)] \}}\\ \end{align*}")
Here the latter term could be accommodated, for instance, by including a spline function of time of entry within the Cox-regression. A similar argument can be made for accelerated failure time models, e.g. a Buckley-James model, in that case the f(t) term can be incorporated into the residual survivor distribution. Similarly, it is easily extended to multiple covariates.
If a parametric model is used under this formulation it is only valid under the assumption that the parametric hazard family applies to the hazard with the deterministic part of the time dependent covariates included, but this is also true for Sperrin and Buchan's approach (assuming f(t) has been estimated correctly).
Having resolved these issues it is still unclear when such a model would be appropriate. It seems that a useful prediction model is only possible from baseline measured covariates if the covariates vary in time in a deterministic way. For truly time-varying covariates, while studies with relatively short follow-up will be able to give reasonable estimates of the effect of the covariate on survival, prediction requires a longitudinal set of covariate observations. Landmarking or multi-state modelling are then possible approaches to account for the time varying covariates. Update: This paper has now been published in Statistics in Medicine (highlighting the quality of their peer reviewers!).
A large proportion of the paper is devoted to arguing that in studies where the entry time does not involve an intervention and follow-up is over a long period, it is more appropriate to use age as the primary timescale rather than using study time and including age at entry as a covariate. The latter approach can lead to counterintuitive results where a 50 year old is more likely to survive to 70 than a 55 year old with the same covariate values except age.
The paper is less convincing when it comes to possible solutions to the problem of time dependent covariates only observed at baseline. Their approach is essentially to assume that
for some arbitrary function f(t). Hence it is assumed that the time dependent covariates vary deterministically so that a subject who has lower than average blood pressure aged 30, will have increasing blood pressure as they age but stay at the same (age specific) quantile. Obviously a first issue is how realistic this is, especially for modelling internal covariates. Assuming this model is correct, Sperrin and Buchan propose a two-step procedure in which they firstly regress the observed baseline covariate values on t to estimate f(t). They then use the residuals from this procedure to put into standard proportional hazards or accelerated failure time models. A problem that they freely acknowledge is that the observed baseline covariate values will be biased if they are, for instance, both increasing with age and associated with increased hazard. They suggest, but don't implement, some form of iterative procedure to accommodate this.
They seem to have overlooked a trivial way around this problem: For a Cox proportional hazards models when f(t) is assumed linear with unknown slope v (as in their example), if we observe covariate value
i.e. the deterministic part of the time dependent covariate is merely absorbed into the baseline hazard and it is just necessary to include age at entry as an additional covariate. For non-linear models we have:
Here the latter term could be accommodated, for instance, by including a spline function of time of entry within the Cox-regression. A similar argument can be made for accelerated failure time models, e.g. a Buckley-James model, in that case the f(t) term can be incorporated into the residual survivor distribution. Similarly, it is easily extended to multiple covariates.
If a parametric model is used under this formulation it is only valid under the assumption that the parametric hazard family applies to the hazard with the deterministic part of the time dependent covariates included, but this is also true for Sperrin and Buchan's approach (assuming f(t) has been estimated correctly).
Having resolved these issues it is still unclear when such a model would be appropriate. It seems that a useful prediction model is only possible from baseline measured covariates if the covariates vary in time in a deterministic way. For truly time-varying covariates, while studies with relatively short follow-up will be able to give reasonable estimates of the effect of the covariate on survival, prediction requires a longitudinal set of covariate observations. Landmarking or multi-state modelling are then possible approaches to account for the time varying covariates. Update: This paper has now been published in Statistics in Medicine (highlighting the quality of their peer reviewers!).
Subscribe to:
Posts (Atom)