Nonparametric inference for competing risks current status data with continuous, discrete or grouped observation times.

Marloes Maathuis and Michael Hudgens have a paper available at arXiv.org. This concerns nonparametric inference for competing risks current status data. They consider a naive estimator, which estimates each cumulative incidence function independently using the pooled-adjacent-violators algorithm. Additionally, the NPMLE is also considered. The naive estimator, while consistent, does not guarantee that the sum of CIFs is less than 1. Moreover, previous work by Groeneboom et al suggests it is less efficient. However, the naive estimator has the advantage (in addition to being computationally simpler) that the limiting distribution of the estimates of each CIF is known (being the same as standard current status survival data) and results regarding the likelihood ratio statistic (Banerjee and Wellner 2005) can be applied to get confidence intervals for the CIFs. These results are in the case of a smooth observation distribution. The authors note that if subjects can only be observed in a (finite) pre-defined grid of time points then obviously the CIFs can only be estimated at these time points but also, since the number of parameters cannot increase indefinitely, standard n^1/2 asymptotics apply.

Related to this work is the R package MLEcens developed by Marloes Maathuis. This computes the NPMLE for bivariate interval censored data. Special cases include competing risks data and standard survival data. Moreover the implementation seems to run considerably faster than the package Icens.

*Update: A video of Marloes Maathuis demonstrating MLEcens is available here.

**Update: The paper is now published in Biometrika.

Robust Estimation of State Occupancy Probabilities for Interval-Censored Multistate Data: An Application Involving Spondylitis in Psoriatic Arthritis

Tolusso and Cook have a paper in Communications in Statistics - Theory and Methods, based on chapter 4 of the first author's PhD thesis. They propose a method of robust estimation for the state occupancy probabilities in progressive multi-state models when the transition times are interval censored. The method is in the spirit of the Pepe estimator being based on the differences between the marginal survival distributions of state entry or exit times. These marginal survival distributions can be estimated either through the NPMLE using self-consistency algorithms, through weakly parametric piecewise-constant hazard assumptions, or via local-likelihood.
The method is applied to a three-state illness death model, where the absorbing state is death and times of entry into the absorbing state are known exactly. Prevalence in state 1 is estimated by the interval-censored survival estimate of exit from state 1, prevalence in state 3 is estimated through the Kaplan-Meier estimate of overall survival and prevalence in state 2 is based on the difference between these functions.
In this case the method can be thought of as a less computationally intensive alternative to using Frydman and Szarek's NPMLE, with the added advantage that it is not necessary to make the Markov assumption.

An unrecognized problem with the method in the case of exactly known death times is that, for the healthy state survival function, the upper boundary of the censoring interval is not independent of the process. If a patient dies then they will be censored in some interval where 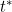is the time of death. However, if they died from state 1, their exit time from state 1 was 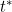. Thus the sojourn time in state 1 will tend to be underestimated and consequentially state 2 occupation will be overestimated. The extent of bias will depend on the chance of death from state 1 and the severity of interval censoring.